Abstract
In this study, relationships between yarn diameter/diameter variation and yarn strength were investigated. For this, we used 100% cotton combed ring yarns of nine types from the same blend which have three yarn counts with three levels of twists, as well as 100% wool worsted yarns of nine types which have nine different yarn counts and twist levels. The findings obtained were evaluated by correlation and regression analyses, and statistically significant correlation coefficients between yarn strength and yarn diameter/diameter variation were found. Furthermore, multiple linear regression models were established to allow the estimation of yarn strength from the other yarn parameters such as yarn diameter, diameter variation, twist, twist variation, capacitive and optical unevenness.
Key words: yarn diameter, yarn strength, yarn twist, optical unevenness, capacitive unevenness.
Musa KılıçMusa Kılıç Ayşe Okur
Introduction
Variation of yarn parameters such as diameter, mass, twist, strength etc. is unavoidable, especially for staple yarns, but this situation is not desired in most cases. Variation of yarn characteristics can cause problems, both during the production processes and after production. So, the relationships between these characteristics must be clearly established in order that precautions may be taken and various problems avoided. Yarn strength is the most important of many yarn parameters. It is in most cases used as a quality parameter of a yarn. Therefore, establishing the relationship between yarn strength and other yarn parameters and estimating the yarn strength is of considerable importance for both practical and theoretical works. In this study, we aimed to investigate the relationships between yarn diameter, diameter variation, twist, twist variation, yarn optical unevenness and yarn unevenness measured by means of a capacitive transducer (capacitive unevenness) and yarn strength experimentally.
Previous studies
Numerous researchers have investigated the relationships between yarn diameter, diameter variation, optical/capacitive unevenness and yarn strength. Among these, Hasler & Honegger [1] investigated the relationships between the capacitive unevenness and strength of cotton ring-spun yarns. It is stated that there is a strong relationship between capacitive unevenness and yarn strength; while the unevenness mentioned above decreases, yarn strength increases. Mandl [2] also
investigated the relationships between yarn unevenness and strength. After theoretical and experimental research, it is stated that yarn strength decreases and the CV% of yarn strength increases where yarn irregularity increases. Lizak [3] used the autocorrelation function technique to establish the dependence of yarn strength on yarn unevenness, and stated that yarn strength decreases where yarn irregularity increases. Başer [4] yarn irregularity increases. Başer [4] found a significant correlation between yarn unevenness and yarn strength, but the expected effect of periodic unevenness to decrease yarn strength was not demonstrated. On the other hand, Shareiff et al. [5] stated that single thread strength falls with an increase in roller eccentricity and drafting level. Penava & Orešković [6] established that correlation between yarn unevenness and yarn strength is unimportant (r = -0.233), although 61 % of yarn breakages occur at thin places along the yarn. In addition, Prendžova [7] stated that 80% of yarn breakages occur at thin places. Cybulska et al. [8] stated that while yarn diameter increases and diameter variation decreases, yarn strength increases. Nanjundaya [9] investigated the strength of cotton ring-spun yarn considering the yarn structure at the region of break. It is stated that most specimens broke at a place where the yarn diameter is minimum and twist is maximum. Ghosh et al. [10] said that yarn failure is strongly dependent on the yarn structure. The results obtained from the experimental work showed that the strength of yarns largely depends on the structure of the yarns, as well as gauge lengths and strain rates. Lappage [11, 12] investigated end breaks in the spinning and weaving of weavable singles yarns.
A good correlation was found between the end breakage rate and the irregularity (CV%) of the yarn, and it is stated that the end breakage rate can be predicted from a knowledge of the unevenness of the yarn, the tension in the spinning balloon and the tenacity of thin places in the spinning triangle.
Material
In this study, the following yarns were used: 100% cotton combed ring yarns of nine types including three different

linear densities (yarn counts), differently treated by twist factor, and 100% wool worsted yarns of nine types differentiated by linear density (yarn count) within the range of 16 tex to 38 tex. Five bobbins were used for each type of cottons, and five packages were used for each type of wools. Yarn counts and twist factors are presented in Tables 1 and 2.
Method
Yarn diameters were measured with a Gaertner M-1170 Micrometer Slide Comparator with 0.001 mm accuracy and 32× magnification. Furthermore, a mechanism which consists of a yarn creel, yarn guides and yarn tensioners was prepared for measuring the yarn diameter under constant tension. The yarn tension was 22 ± 1 cN for all of the yarn types, so that the effect of yarn tension on yarn diameter could be assessed.
For diameter measurements, a 250-mm yarn length was marked, and the yarn diameter was measured from 10 different points of this marked piece. For each bobbin or package, this operation was repeated 20 times and 2 m of yarn was unwound between each marked piece.
The yarn strength measurements were performed in synchronisation with the yarn diameter measurements. After measuring the yarn diameters, a marked yarn piece of 250 mm was tested at 250-mm test length on the tensile tester. So, diameter-strength measurements were performed 20 times for each bobbin or package, and 100 times for each yarn type .
The yarn twist measurements were also performed in synchronisation with the yarn diameter measurements. After measuring the yarn diameters, the marked yarn piece of 250 mm was tested at 250-mm test length on the twist tester. So, diameter-twist measurements were performed 20 times for each bobbin or package and 100 times for each yarn type .
For each bobbin or package, the optical and capacitive unevenness measurements were performed on a Superba RTF 6F Yarn
Tester, and optical (%CVOPT) and capacitive (%CVCAP) unevenness values and frequently occurring faults (thin places, thick places and neps) were obtained.
Yarn counts were measured by using yarn reel. For each bobbin or package 3 measurements were performed, and for each measurement 50 m yarn was unwound.
To analyse the results, correlation and multiple linear regression analyses were applied to the test results obtained.
Results and discussion
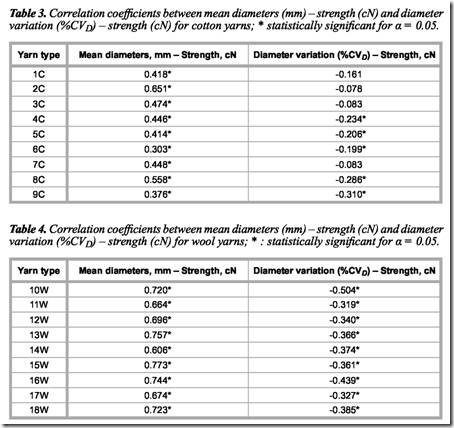
The test results obtained by diameter-strength measurements were evaluated by correlation analysis. The correlation coefficients at significance level of α = 0.05 between mean diameters (mm) – strength (cN) and diameter variation (%CVD) – strength (cN) are presented in Tables 3 and 4 for cotton and wool yarns. As seen from the tables, both for cotton and wool yarns, statistically significant correlation coefficients exist between the mean diameters (mm) and strength (cN). As stated by Penava & Orešković [6], As stated by Penava & Orešković [6], As stated by Penava & Orešković [6], Prendžova [7] and Cybulska et al. [8], if the mean diameter increases, the yarn strength increases. However, the relationship between diameter variation
(%CVD) and strength (cN) is significant only for 4C, 5C, 6C, 8C, and 9C types of cotton yarns, but significant for all types of wool yarns. As stated by Cybulska [8], if the yarn diameter variation increases, the yarn strength decreases. Mean diameters (mm) – strength (cN) and diameter variation (%CVD) – strength (cN) diagrams of types 4C and 10W are shown in Figures 1 to 4.
When Figures 1 to 4 are examined, it is seen that yarn strength decreases at the regions where yarn diameter decreases. If it is thought that the tension which a yarn can carry depends on the number of fibres at the cross-section and friction forces between the fibres, then a decrease in yarn strength at the regions where the yarn diameter, and consequently the number of the fibres at the cross-section decreases, as well as a statistically significant relationship between yarn diameter variation can be both accepted as the expected results.
To establish the relationships between the diameter variation (%CVD) and strength variation (%CVS)/twist variation (%CVT) of the yarns, diameter variation and strength variation/twist variation values of the bobbins or packages were evaluated by correlation analyses. Significant correlation coefficients at a significance level

of α = 0.05 between diameter variations of α = 0.05 between diameter variations (%CVD) and strength variations (%CVS) were determined both for cotton and wool yarns. Correlation coefficients were 0.402 for cotton yarns and 0.612 for wool yarns. As stated by Mandl [2], the CV% of yarn strength increases where the yarn irregularity increases. In this study, it is posited that the CV% of yarn strength increases where the yarn diameter variation increases. Figure 5 and 6 illustrate diameter variation (%CVD) – strength variation (%CVS) for cotton and wool yarns.
When analysing the relationships between yarn diameter/diameter variation and strength, the effect of twist on diameter and strength must be considered. It is generally known that more twist takes place at thin places in ring spun yarns.
This is because there are fewer fibres at thin places, and resistance to torsion is less in these regions. However, an opposite situation exists at thick places. So, in most cases less twist takes place at thick places. In this study, the relationships between mean diameters (mm)–twist (T/m) were also investigated, and statistically significant correlation coefficients at a significance level of α = 0.05 were at a significance level of α = 0.05 were found both for cotton yarns (minimum -0.211 for type 1C and maximum -0.638 for type 7C) and wool yarns (minimum - 0.438 for type 11W and maximum -0.868 for type 17W). Correlation coefficients between diameter variations (%CVD) and twist variations (%CVT) were found to be statistically significant for wool yarns (0.710), but not significant for cotton yarns (0.081).
On the other hand, multiple linear regression models were established to estimate the yarn strength (S, cN) from other yarn parameters such as yarn diameter (D, mm), diameter variation (%CVD), twist (T, T/m), twist variation (%CVT), capacitive unevenness (CAP, %CV) and optical unevenness (OPT, %CV). Some of the multiple linear regression models calculated for cotton and wool yarns are presented below. For cotton yarns, these equations were as follows:



with adjusted R square values of 0.847, 0.946 and 0.945. Similar equations were also calculated for wool yarns:

with adjusted R square values of 0.932, 0.939 and 0.954.
If capacitive and optical unevenness values are used as independent variables instead of diameter values measured with the method mentioned in this study in the above equations, then Equations (7) - (14) are obtained with adjusted R square values of 0.795, 0.806, 0.792, and 0.800 for cotton yarns and 0.804, 0.812, 0.816, and 0.871 for wool yarns respectively.

The adjusted R square values for Equations 1 - 6 are generally higher than Equations 7 - 14. This shows that the multiple linear regression models which contain the parameters calculated by the method used in this study provide a better estimation of yarn strength.
Strength, one of the most important quality characteristics of yarn, can be estimated from parameters such as yarn diameter, diameter variation, twist, twist variation, capacitive and optical unevenness. In Figures 7 and 8, correlations between estimated and experimental values of yarn strength are presented for cotton and wool yarns. Equations (3) and (6) were used for the comparison and estimation of yarn strength. The correlation coefficients between the estimated and experimental values of yarn strength, r = 0.975 for cotton yarns and r = 0.979 for wool yarns, show the usefulness and precision of the multiple linear regression models which were calculated.
For example, the yarn diameter (D) was 0.195 mm, the diameter variation (%CVD) was 10.6%, the twist (T) was 751 tpm and twist variation (%CVT) was 2.3% for a 25 tex 100% cotton combed ring yarn. By using Equation (3), the yarn strength is calculated as 380.3 cN. From the experimental work, the mean yarn strength for 20 tests was obtained as 373.6 cN. It is clearly seen that the model fits the reality with a fairly high percentage. Similarly for a 21 tex 100% worsted wool yarn, the yarn strength is calculated as 124.5 cN by using Equation (6), and the experimental result was 130.5 cN.
Conclusion
In this study, relationships between yarn diameter measured with the optical method (as defined in the Method section) and yarn strength were investigated. As stated by Penava & Orešković [6], Prendžova [7], strength were investigated. As stated by Penava & Orešković [6], Prendžova [7], Cybulska et al. [8], Nanjundaya [9] etc., yarn strength decreases at the regions where yarn diameter decreases. A decrease in yarn strength at the regions where yarn diameter, and consequently the number of fibres at the cross section will decrease, together with statistically
significant relationships between yarn diameter variation and strength variation, can be accepted as expected results. In addition, multiple linear regression models were established to estimate yarn strength from other yarn parameters such as yarn diameter, diameter variation, twist, twist variation, capacitive and optical unevenness, and fairly high adjusted R square values were obtained. It is expected that the experimental findings and statistical analyses resulting from this study will contribute to studies on relationships between yarn parameters and estimating yarn strength from other yarn parameters.