Process Parameters
Abstract
This work presents an analysis of the quality parameters of cotton yarns with linear densities of 15, 18, 20, 25, 30, and 40 tex manufactured with the use of ring-, compact-, and BD 200S & R1 rotor spinning machines. Slivers and rovings obtained from carded and combed middle-staple cotton were the initial half-products. We determined the functional dependencies of selected fundamental parameters of yarn quality, such as tenacity, elongation at break, unevenness of linear density, hairiness and the number of faults on the yarn’s linear density. The dependencies assessed allow us to calculate the quality parameters of cotton yarns for any given linear mass, and enable the modelling of yarn parameters for different carded and combed yarn streams spun with use of the various spinning machines which were the object of this research.
Key words: cotton, combed cotton yarn, carded cotton yarn, ring spinning, compact spinning, rotor spinning, quality yarn parameters, linear regression, non-linear regression, mean-square approximation.
Introduction
The process of converting fibres into yarn is complex, and requires many investigations and new technical & technological solutions. The importance of this problem is confirmed by the publications of foreign authors. El-Mogahzy worked on the broad field of questions of yarn engineering [4]. Kim attempted to estimate yarn quality on the basis of its external view [ 14]. Ben-Hassen and Renner carried out research on high drawings applied in cotton spinning, and their influence on yarn quality [3].
Research on compact yarns, their quality, and the structure of compact and classical yarns is found in the work of Jackowski, Cyniak, & Czekalski [10], Krifa & Ethridge, and Basal & Oxenham [2]. Hyrenbach investigated the structure of rotor yarns and the advantages of applying them in textile products [5].
The cotton yarns manufactured in Poland are faced with strong competition from yarns manufactured in India, Turkey, and China which have recently appeared on the Polish domestic market. In order to improve the quality level of the yarns manufactured, Polish domestic manufacturers have implemented a series of new investments including the purchase of new machines, such as opening & cleaning machines, carding machines, sets of combing machines, and new types of spinning frames. At present, as a result of these attempts, Polish yarns are of equal quality, or even better, than imported yarns.
The authors are aware that it is possible to improve the quality of cotton yarns manufactured in Poland even further by combing the middle-staple length cotton, increasing the regularity of half-finished products, such as slivers & rovings, and using new types of spinning frames [12]. The investigations described in this article are a continuation of the research carried out by the authors on yarn quality and modelling the spinning process [6 - 9]. Special expectations are connected with the use of compact ring spinning frames in classical spinning and the R1 rotor spinning frames of the third generation of spinning machines in the rotor spinning process [6]. Tests with the use of a classical PJ ring-spinning frame and the BD 200S rotor-spinning machine were carried out in order to obtain valuable comparative results.
Middle-staple cotton with a staple length of 32/33 mm, a linear density of 165 mtex, a tenacity of 24.9 cN/tex, and an elongation at break of 7.7% were used as the raw material for our research. Slivers with a linear density of 4.45 ktex and roving with a linear density of 600 tex were the initial half-products. The slivers were prepared from middle-staple cotton, which was carded and combed, with a percentage of noils at the level of 24%.
Yarns with linear densities of 15, 18, 20, 25, 30, and 40 tex were manufactured from the slivers and rovings prepared with classical and compact ring spinning frames, as well as the BD 200 and R1 rotor spinning machines. All the yarn
variants were laboratory-tested in order to assess such yarn quality parameters as linear density, number of twists, breaking force, elongation at break, work (energy) up to break, specific strength, unevenness of linear density, hairiness, and the number of faults. All tests were carried out in the laboratory of the Department of Spinning Technology and Yarn Structure at the Technical University of Łódź, ture at the Technical University of Łódź, and documented in the elaboration of this research project. The tests of number of twists, specific strength, and work up to break were carried out only in order to establish those comparative yarn features which would allow us to check the repeatability of the yarns processed, and was not considered in the analysis presented in this article.
Aim of research
The basic aim of our research was to determine the influence of the type of carded or combed slivers which fed the spinning machine, and of the linear density of the yarn manufactured, on the quality parameters of yarns produced with the use of modern spinning frames, as well to determine the functional dependencies which would enable us to model the influence of changes to the tested spinning process parameters on the yarn quality.
Partial models of the spinning process were developed for selected essential quality parameters, such as the yarn’s unevenness of linear density, the tenacity, the hairiness, and the number of faults, which enable the values of these parameters to be determined in dependence on the linear density of the yarn manufactured. The knowledge a priori about the spinning process and the results of the experimental research carried out were used to determine the desired functional dependencies.
Modelling the unevenness of the linear density of yarn
We investigated the dependence of the coefficient of variation of the yarn linear density CVy on the yarn linear density Tt for different kinds of cotton yarns and various types of spinning machines. This dependency has a non-linear character (Figure 1 see page 27), and can be approximated by functions of the following form [4]:

Calculation of the theoretical value of the coefficient of variation of the yarn’s linear density CVT on the basis of Equations (2) and (3), and its substitution as a variable into Equation (1), enabled the desired dependency to be linearised. The values of the coefficients C0 and C1 of the function (1) were assessed by the least-squares method [7]. Their value for different yarn and machine variants are presented in Table 1. The estimators of the standard deviation SCV of the variable CVy, accepted as an independent variable, were also determined, which means assessing the measuring uncertainties of determining the coefficient of variation CVy, the standard deviations SC0 and SC1 of the coefficients determined, and the linear correlation coefficient r between the variable CVy and CVT. The calculation results are listed in Table 1. The value of the coefficient r confirm the very strong correlation dependency and the correct selection of the auxiliary variable CVT. Figure 1 presents the measurement results and the dependencies determined for the classical ring spinning frame (PO), the compact ring spinning frame (PK), and the BD 200S & R1 rotor spinning machines.
From the dependencies presented in Figures 1.a and 1.b. the self-evident con-
clusion results that the unevenness of the yarn’s linear density decreases with the increase in linear density according to Equations (1) and (2). The unevenness of combed yarns is smaller than that of carded yarns, and this is the cause of the improvement in quality of the former. It is interesting to note that the unevenness of carded compact yarns is very similar to that of carded rotor yarns, even though the fibres in the compact ring frame are fed through the drawing apparatus. The smaller unevenness of yarns manufactured with the use of the R1 spinning frame in relation to the yarns obtained by the BD 200S frame results from the use of Uster Polygard systems on each spinning position of the R1 spinning frame.
Modelling the tenacity of yarn
The yarn’s tenacity WW is one of the most significant yarn parameters which is decisive for breakages during the processes of spinning, winding, warping, weaving, and knitting, as the yarn breakage depends on the machines’ efficiency and product quality.
The dependency of tenacity on the linear density of yarn was determined by experimental means, and modelling was carried out with the use of linear regression [8, 13]:
The values of coefficients a1 and a0 were determined by the least-squares method. Their values for different yarn variants and various machines, the estimators of the standard deviation SW of the variable Ww, the standard deviations Sa1 & Sa0 of the coefficients determined, and the coefficients of linear correlation r are listed in Table 2.
The values of the coefficient r within the range of (0.9-1.0) confirm a very strong



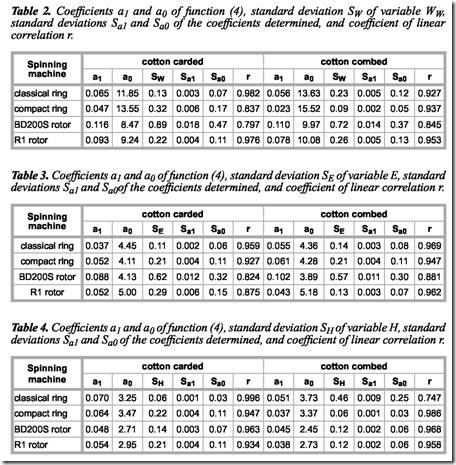
correlation dependency between tenacity and linear density of yarn, and within the range of (0.7-1.0) a strong correlation dependency, as well as the correct selection of the linear regression model (4).
Figure 2 presents the measurement results and the dependencies determined for the classical ring spinning frame (PO), the compact ring spinning frame (PK), and the BD 200S & R1 rotor spinning machines. From these dependencies, the distinct influence of the spinning machine type on the yarn tenacity can be seen. Yarns obtained by the classical and the compact ring spinning frames have the fibres arranged in parallel and straightened in the drawing apparatus of the frame, which causes their tenacity to increase. The process of arranging the fibres in yarn proceeds most advantageously in the compact apparatus of the frame. The yarn tenacity increases with the increase in the yarn’s linear density. Combing cotton also increases the tenacity of about 1-2 cN/tex.
Modelling the yarn’s elongation at break
The elongation at break E was analysed together with the yarns’ tensile strength
properties and with their tenacities. It is important that the elongation at break is not too small, as in such a case the yarn will break while winding.
The dependency of elongation at break on the yarn’s linear density was modelled with the use of linear regression (4). The values of coefficients a1 and a0 for different yarn variants and various machines, the estimators of the standard deviation SE of the variable E, the standard deviations Sa1 and Sa0 of the coefficients determined, and the coefficients of linear correlation r are listed in Table 3. The values of the coefficient r within the range of 0.8-1.0 confirm a strong correlation dependency between elongation at break and linear density of yarn, as well as the correct selection of the linear regression model (4).
Figure 3 presents the measurement results and the dependencies determined for the classical ring spinning frame (PO), the compact ring spinning frame (PK), and the BD 200S & R1 rotor spinning machines. From these dependencies it results that the elongation at break increases with the increase in the linear density of the yarn. In contrast to tenacity, the elongation at break is smaller for yarns
obtained from classical and compact ring spinning frames than for rotor yarns. The fibre arrangement in rotor yarns is worse; during opening the fibres are torn off, followed by initial straightening and tensioning, and next they are broken.
The influence of the combing process on the value of the elongation at break is total unimportant.
Modelling yarn hairiness
According to Barella, yarn hairiness H is one of the more important parameters influencing the yarns’ usability from the point of view of the appearance of the final products [1]. We measured the hairiness with the Uster apparatus.
The dependency of hairiness on the yarn’s linear density was modelled with the use of linear regression (4). The values of coefficients a1 and a0 for different yarn variants and various machines, the estimators of the standard deviation SH of the variable H, the standard deviations Sa1 and Sa0 of the coefficients determined, and the coefficients of linear correlation r are listed in Table 4.
The value of the coefficient r within the range of (0.9-1.0) confirms a very strong correlation dependency between hairiness and the linear density of yarn, as well as the correct selection of the linear regression model (4). Only for the case of the ring spinning frame and combed cotton does the r-value confirm a strong dependency.
From the dependencies presented in Figures 4.a and 4.b, it results that the yarn hairiness of classical and compact ring yarns, both carded and combed, is higher than that of rotor yarns. The yarn hairiness increased with the increase in yarn linear density for all the yarns we tested, as the number of fibres in the yarn cross-section increases.
Modelling the number of thin places
Yarn faults in the shape of thin & thick places and neps are decisive on the external appearance of yarns and the products obtained from them. An optimum solution is the possible smallest number of faults.
The number of thin places p on the yarn’s linear density was modelled by the method of non-linear regression. The possibility of using different functions was tested. Calculations were made for



polynomials of the 1 st, 2nd, and 3rd order, exponential functions of the 1 st and 2nd order, the functions described by Equations (1 - 3), the inverse function, and the functions which are derivatives of the latter. The minimum of the sum of the mean square error approximation for all yarn types and the machines used was selected as the criterion for selecting the best dependency form to be accepted for use in our modelling. The best solution of approximation was obtained for the following equation:
After substituting the auxiliary variable x to Equation (5), a model of polynomial
regression was obtained. The values of coefficients B2, B1, and B0 for the different spinning methods were determined by the mean square approximation. The estimators of standard deviation Sp of the variable p, and the linear correlation coefficient r and parabolic coefficient R [13] between the variable p and the auxiliary variable x were also calculated. The calculation results are listed in Table 5.
The values of the coefficient r are within the range of (0.86-1.0), and those of R within (0.92-1.0). This indicates that the

model of parabolic regression is better and of greater accuracy when used for investigating the dependency under discussion than that of linear regression.
Figure 5 presents the measurement results and the dependencies determined for the classical ring spinning frame (PO), the compact ring spinning frame (PK), and the BD 200S & R1 rotor spinning machines. From these dependencies, it results that the number of thin places of the yarn decreases with the increase in the yarn’s linear density, according to Equation (5). The highest number of faults appears in the thinnest yarn with a linear density of 15 tex, in which the number of fibres in the yarn cross-section is the smallest. What is more, thin yarns have the highest unevenness, and the faults are more clearly visible. We obtained the worst results for carded yarns manufactured with the use of classical ring spinning frames. Combed yarns were characterised by a very low number of faults.
Modelling the number of thick places
The dependency of the number of thick places z on the linear density of yarn was approximated by the function (5) with the basic function (6), which were selected to approximate the dependency of the number of thin places on the linear density.
The values of coefficients B2, B1, and B0 of the function (5) for the different spinning methods determined by the mean square approximation and the estimators of standard deviation Sz of the variable z, and the linear correlation coefficient r and parabolic coefficient R [13] between the variable z and the auxiliary variable x are listed in Table 6.
The values of the coefficients r and R are similar and fall within the range of (0.92-1.0). On this basis, a solution was devised to reduce the model of parabolic regression to the model of linear regression. The calculation results are listed in Table 7.
The measurement results and the dependencies determined for the classical ring spinning frame (PO), the compact ring spinning frame (PK), and the BD 200S & R1 rotor spinning machines for the mod-
el reduced are presented in Figure 6. As for the thin places, the greatest number of thick places is visible on the 15 tex yarn. The thicker yarns with linear densities of 35 tex and 40 tex have smaller numbers of thick places.
Thanks to the removal of the short fibres and impurities, the combed yarns have lower number of thick places by several
times. The worst results were obtained for yarns produced on the classical ring spinning frame.
Modelling the number of neps
The dependency of the number of neps n, on the yarn’s linear density was approximated by function (5) with the basic function (6), which were used for approximating the dependencies of the
number of thin and thick places on the linear density.
The values of coefficients B2, B1, and B0 of the function (5) for the different spinning methods determined by the mean square approximation and the estimators of the standard deviation Sn of the variable n, and the linear correlation coefficient r and the parabolic coefficient R [13] between the variable n and the auxiliary variable x are listed in Table 8. The values of the coefficients r and R are similar and fall within the range of (0.85-1.0). On this basis, a solution was devised to reduce the model of parabolic regression to the model of linear regression. The calculation results are listed in Table 9.
The measurement results and the dependencies determined for the classical ring spinning frame (PO), the compact ring spinning frame (PK), and the BD 200S & R1 rotor spinning machines for the model reduced are presented in Figure 7. The dependencies presented confirm the similarity of the neps’ distribution to the distributions of thin and thick places.
The smaller number of faults in yarns manufactured with the use of the R1 spinning frame in relation to yarns obtained by the BD 2005 frame results from using Uster Polygard systems on each spinning position of the R1 spinning frame.
Summary and conclusions
For selected essential yarn quality parameters, the functional dependencies of these parameters on the linear density of the yarns manufactured were determined.
The non-linear dependency of the coefficient of variation of the yarn’s linear density on the value of the linear density was linearised using the Martindale equation and the a priori knowledge about the spinning process.
The functional dependencies for the remaining parameters were determined on the basis of experimental research.
The dependencies of tenacity, elongation at break, and hairiness on the yarn’s
linear density, which were modelled with the use of linear regression, confirmed a strong or very strong correlation between the parameters tested and the linear density. With the increase in the linear density, the tenacity, the elongation at break, and the hairiness also increase.
The dependency of the number of faults, i.e. thin & thick places and neps, on the linear density of yarn was modelled by non-linear regression (5). The analysis of the coefficients of linear and parabolic correlation and of the dependencies established enabled a reduction of the model’s order in the case of thick places and neps. With the increase in the yarn’s linear density, the number of faults decreases.
Yarns manufactured by the EliTe compact spinning frame in comparison with yarns manufactured by the PJ spinning frame are characterised by higher tenacity, smaller unevenness of their linear density measured on short segments, a significantly smaller number of thin & thick places and neps; as well as by a higher degree of elasticity, and fundamentally lower hairiness.
Combed compact yarns have a lower tenacity, a smaller unevenness of the linear density, and a smaller hairiness in comparison to carded compact yarns.
The lower unevenness of the linear density of yarns manufactured with the use of the R1 spinning frame, and their smaller number of faults in comparison with yarns manufactured with the BD 200S spinning frame, is the result of using Uster Polygard systems on each spinning position of the R1 frame.
The rotor yarns are characterised by significant quality parameters, such as unevenness of linear density, the number of faults, and hairiness, which are better than those of ring yarns, and can be accepted as yarns of high quality.
The quality of the spun yarn can be significantly improved, while using equally raw material, by a suitable selection of the spinning system and the type of the spinning machine used.