FRAGMENTED LOW-ELONGATION FIBERS
ABSTRACT
Often, fibers with significantly different elongations-to-break are combined in blended yarns. During yarn extension, the low elongation-to-break (LE) fibers undergo a fragmentation process, whereby the LE fibers develop multiple breaks along their length. The interaction between the LE fragments and the high elongation-to-break (HE) fibers is key to the load-extension behavior of such blended yarns. In this work, a micro-mechanical model for the interactions in a mixed array of elastic fibers representing the microstructure of a blended yarn undergoing axial extension is adopted and modified for the assumption of hexagonal fiber packing. The present results, which represent essentially an upper bound on the mechanical behavior that can be attained by increasing packing density, are compared to previous results for the assumption of square packing. It is shown that increased packing density provides for better reinforcement of the yarn by the LE fragments.
KEY WORDS: fragmentation process, hybrid yarn, fiber friction, shear lag model, hybrid effect, yarn mechanics, rope, hexagonal packing.
1. INTRODUCTION
There is renewed interest in modeling the mechanical behavior of blended yarns, as reflected in recent papers by Realff et al. (2000), Godfrey and Rossettos (2001), and Rossettos and Godfrey (2002). While the works by principal authors Godfrey and Rossettos consider blended yarn behavior at
the microstructural level, Realff et al. develop a stochastic model that treats the entire yarn. In general, these works aim to investigate how blended yarn load-extension behavior is affected by the interactions occurring between the constituent LE and HE fibers. A key issue is the possible exploitation of beneficial “hybrid effects” whereby the LE fibers may be used to carry
loads in the yarn at strains exceeding the failure strain of a homogenous LE fiber yarn (Rossettos and Godfrey, 2002). Realff et al. (2000) and Godfrey and Rossettos (2001) discuss the successive fragmentation of LE fibers that occurs in blended yarns. These phenomena have close parallels in the mechanics of fiber-reinforced composites. Recognizing this, some authors have used twisted blended yarns as surrogates to elucidate the behavior of hybrid fiber composites (Monego et al., 1994; Pan et al., 1998). Clearly, research can be adapted in the opposite direction as well, and given the wealth of research activity over several decades in fiber-reinforced composites, blended yarn mechanics is well positioned to benefit. In particular, sophisticated statistical theories developed for fiber composites could be modified, using results and insights attained in the present and referenced works, to develop predictive theories for the stress-strain and strength behavior of blended yarns. Representative works in statistical theories for composites, treating complex mechanistic aspects such as fiber fragmentation, frictional slip of fibers, matrix cracking, and matrix yielding, include Curtin (1991, 1993), Nuemeister (1993), Phoenix et al. (1996), and Hui et al. (2000).
The present work concerns the extension of blended yarns undergoing fragmentation of the LE fibers. In the case that the LE fibers are significantly stiffer than the HE fibers, the fragmentation of the LE fibers may lead to a large drop in tension on the yarn as the yarn is extended in the post-fragmentation regime. For high strength yarns, it is desirable, therefore, that the LE fragments continue to reinforce the yarn and contribute to the overall stiffness and load-carrying ability. This is an important problem commercially because of the large quantities of blended staple yarns produced for apparel. However, tailoring of strength and stiffness properties through intimate blending of different fiber types may be useful in technical textiles as well. In high performance ropes, for example, it may be possible to design a rope with high initial stiffness in combination with high toughness and elongation-to-break by blending stiff LE fibers with compliant HE fibers. Yarns created with such a combination of properties may also have application to woven fabrics used for soft body armor.
In this paper, we adopt a micromechanical model for the extension of a hybrid fiber array representing the microstructure of a hybrid yarn undergoing fragmentation of the LE fibers (Godfrey and Rossettos, 2001) and modify the model for the assumption of hexagonal fiber packing. The parallel mixed array of elastic fibers consists of a small fraction of relatively high-modulus, LE fibers dispersed among HE fibers. The LE fibers are assumed to break into fragments that slip relative to neighboring fibers in regions near the fragment tips; analysis of frictional slip forces acting in the slip region is motivated by results for yarn internal stresses (Hearle et al., 1969, pp. 175-212). The model is used to investigate the contribution of the LE fragments to the load-carrying ability of the fiber array. The present results are compared to previous results for the assumption of square packing. It is shown that increased packing density provides for better reinforcement of the yarn by the LE fragments. In addition, peak strains in HE fibers are shown to be reduced in hexagonal versus square packing, suggesting that more densely packed yarn microstructures may sustain higher extension prior to complete failure.
2. MICROMECHANICAL MODEL
We adopt a micromechanical model, introduced by Godfrey and Rossettos (2001) under the assumption of square fiber packing. In this section, the main elements of the model are summarized, and the model is specialized for the hexagonal packing assumption.
Consider a uniformly blended twisted yarn composed of a small fraction of LE fibers dispersed among HE fibers. The yarn is assumed to possess the well accepted idealized helical structure (Hearle et al., 1969, pp. 65-67) where the fibers lie in coaxial concentric layers and follow helical paths. The tangent of the helix angle varies linearly with radial position in the yarn from
zero at the center to a maximum on the yarn surface. Directing our attention to the central region of the yarn, the fibers are nearly parallel to the yarn axis. Fibers near the yarn's center, therefore, experience the highest strains during yarn extension and yarn rupture usually initiates in the central region.
As yarn tension increases, lateral compression drives the local packing toward a regular periodic structure. However, fiber migration, the tendency for the twisted yarn under tension to assume a circular cross-section, and size and shape differences between the LE and HE fibers necessitate that the fiber array deviate from a perfect lattice through packing flaws. For parallel fibers with identical circular cross-sections, hexagonal packing provides the maximum possible fiber packing density. As such, the behavior exhibited by hexagonally packed fiber arrays may be regarded as an upper bound on the mechanical behavior of fiber arrays with increasing fiber packing densities.
Consider a hexagonally packed mixed array of parallel linearly elastic fibers representing the local microstructure of the yarn near the yarn's center. For hybrid yarns containing sufficiently small fractions of LE fibers, we assume the LE fibers are far enough apart that their regions of influence do not overlap. The LE fibers are assumed to develop evenly spaced breaks such that they form fragments of uniform length 2 l. Based on these assumptions, we investigate the behavior of a finite section of the fiber array of length l comprised of one-half of a single LE fiber fragment embedded in the center of a hexagonal region of HE fibers. This finite section is essentially a unit cell of the fiber array. The x-coordinate axis is parallel to the fiber direction, with the origin placed at a LE fragment tip. The LE and HE fibers are assumed to be approximately transversely isotropic. Based on similar calculations with square packing (Godfrey and Rossettos, 2001), results are not particularly sensitive to number of layers of HE fibers surrounding the LE fragment that are included in the unit cell. In this work, three layers of HE fibers are included in the hexagonal unit cell, Figure 1. Due to symmetry, only six fibers need to be independently represented in the model; these are shown in red (LE fragment) and white (HE fibers) in Figure 1. The fiber array is extended in the x-direction to a nominal strain a.

The general form of the fiber equilibrium equation in a square-packed array is derived in detail by Godfrey and Rossettos (2001). To derive equations for the six independent fibers in the hexagonal unit cell (Figure 1) we proceed as follows, starting with the center LE fragment. The fiber array is laterally compressed, due to the interaction of yarn tension and twist, so that fiber-to-fiber load transfer may occur via surface friction. Along the contact line with each of its six abutters, a contact "shear flow" is applied to the LE fragment (the LE fragment is denoted fiber number 0). The term "shear flow" is used here to connote a force per unit length. Figure 2 illustrates axial equilibrium of an arbitrary fiber under the influence of the shear flows from abutting fibers. HE fibers each have an effective axial stiffness E*A* and the LE fiber has an effective axial stiffness EA. We denote the shear flow from fiber 1 to fiber 0 along the contact line as q1,0 and take the convention that positive shear flows to a fiber act in the positive x-direction on that fiber. By symmetry, fiber 0 experiences six
identical shear flows from its interaction
with its six abutters. Introduce u„ as the
average axial (x-direction) displacement in
fiber n at position x. It is convenient to take
as the displacement reference the position of
points on an undamaged fiber array (LE
fiber is not fragmented) under the same
nominal strain. For HE fibers, the axial force
due to LE fiber fragmentation is
E * A * (du„ dx) and the axial force in the LE
fragment due to fragmentation
is EA(du0 dx) . From the free body diagram,
Figure 2, axial equilibrium for the LE fragment can, therefore, be written as,

No Slip Between Fibers
We assume that, given that no slip occurs at the contact surface, the shear flow at the contact line between two abutting fibers may be considered linearly proportional to the difference in the fibers' average axial displacements (Godfrey and Rossettos, 2001). For a contact line between an HE fiber and the LE fiber, we denote the proportionality constant k, and use k* for contact lines between two HE fibers. For the shear flow q1,0, the contact line is between an HE fiber and the LE fragment, so we write the shear flow as,
where a positive shear flow occurs on fiber 0 when the displacement of fiber 1 exceeds that of fiber 0.
The proportionality constants k and k* involve the shearing of fibers longitudinally due to surface tractions along the fiber-tofiber contact lines. Treating the fiber material as a homogenous solid, the stiffness constant k* will be proportional to the HE material’s shear modulus in the longitudinal-transverse plane, GLT. The constant k will involve the shear moduli of both fibers in a springs-in-series arrangement. Measurements of the shear modulus of a variety of textile fibers are tabulated in the book by Morton and Hearle (1975, p. 418, p. 428). These range from 0.33 to 1.6 GPa. Physical reasoning suggests the value of k* should be somewhat less than the value of GLT for the HE fiber material, since the packed array of HE fibers may be regarded as a porous solid.
In Figure 1, shaded fibers abutting the red and white fibers are also shown numbered to indicate the symmetry conditions. For example, in considering the shear flows acting on fiber 1, we note that fiber 1 has six abutters, therefore, the potential exists for six shear flows to act on it. However, two of the abutters (shown shaded and marked 1) have by symmetry the same displacement as fiber 1, therefore, no shear flows arise along these contact lines. The shear flow arising from contact with the shaded fiber numbered 3 will by symmetry be equal in magnitude to the shear flow arising from the fiber 3 shown in white. Summing the shear flows acting on fiber 1, the equilibrium equation is written as,

Equilibrium equations for fibers 2 through 5 may be derived in a similar manner. For fibers 4 and 5, on the outer ring of the unit cell, it is assumed that no shear flows arise from contact with fibers outside the unit cell boundary. For conciseness, only the final, non-dimensionalized form of the equilibrium equations for fibers 2 through 5 will be given here.
Introduce dimensionless position
coordinate ~ and displacements U„ defined
by

Putting Equation 2 into Equation 1 and Equations 4 into Equation 3, and nondimensionalizing, using Equations 5, dimensionless equilibrium equations for fiber 0 (LE fragment) and fiber 1, are written as,
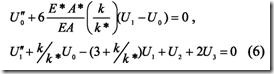
respectively, where primes denote
differentiation with respect to ξ. Similarly, the dimensionless equations for fibers 2 through 5 are written as,
U2 ′′ + ′′ + ′′ +U1 − −6U2 +2U3+ U4 +2U5 = 0,
U3′+ 2U1 + 2U2− 6U3+ 2U5 = 0,
U4′′′′ + U2− 3U4 + 2U5 = 0,
U5′′′′+ U2+ U3+ U4− 3U5= 0. (7)
Frictional Slip Of The LE Fragment
We assume that slip occurs between the LE fragment and the abutting HE fibers in a
region near the LE fragment tip, 0 ≤ x < a,
where a is less than l. The shear flow acting along each slipping contact line is denoted qs. Axial equilibrium of the LE fragment in
the region 0 ≤ x < a is written as
where the fragment slips relative to six abutting HE fibers.
The interaction of yarn twist and remote tension on the yarn gives rise to lateral compression within the yarn. As in Godfrey and Rossettos (2001), we assume Amontons’ Law behavior at the slipping contact lines so that the contact line slip shear flow, qs, is proportional to the contact line compressive force per unit length. Since the compressive forces are induced by yarn tension, the slip shear flow is to a first approximation proportional to the nominal strain, ε . Godfrey and Rossettos (2001) showed that the slip shear flow in square-packed arrays could be estimated as,
where µ is the coefficient of friction
between slipping LE and HE fiber surfaces,
d is the average fiber layer-to-layer spacing, E is the axial modulus of the fiber array where the array is smeared out into an effective homogeneous solid (units of
force/length2), and η is a function of yarn
surface helix angle and radial position of the fiber array within the yarn that determines the ratio of lateral compressive stress to axial stress on the fiber array.
Using Equations 5, Equation 8 may be nondimensionalized, giving,

In the second of Equations 11 we have used Equation 9. The parameter Q is seen to involve only properties of the constituent fibers, properties of the smeared fiber array, the position of the array within the yarn and
the yarn twist (through η). Therefore, Q may
be regarded as somewhat of a material property of the hybrid yarn. In the hexagonal array, the parameter d must be interpreted as a factor, having units of length, that relates the mean contact line compressive force/length to the lateral compressive stress in the fiber array. While Equation 11 suggests microstructural properties that are involved in Q, Q should be regarded as an empirical parameter, ultimately to be calibrated through appropriate experiments.
For fiber 1, frictional slip occurs along its contact line with the center LE fragment, but it is assumed no slip occurs between it and its other three abutters. The dimensionless equilibrium equation may be obtained from the equation for the non-slipping region, the second of Equations 7, by replacing the terms arising from the elastic interaction with fiber 0,
(U0 − − U1) k k * , with +Q, representing the
frictional slip shear flow acting on fiber 1 in the positive x-direction (the LE fragment slips in the + x-direction). Therefore,
equilibrium of fiber 1 in the region 0 ≤ x < a
may be written as,





Load Contribution Of LE Fragment



expected, longer fragments exhibit higher load contributions than shorter fragments. The hexagonal packing case exhibits higher LE fragment load contribution than the square packing case for given values of Q. Higher values of load contribution indicate better reinforcement of the yarn by the LE fragments. These results suggest that both the packing density, reflected here in our study of hexagonal versus square packing, and the parameter Q, are important material properties to consider in the design of blended yarns intended to support high loads during fragmentation.
Peak Fiber and Fragment Strains
When the fragmented fiber array is extended, local axial strains in each fiber/fragment distribute themselves such that the fiber array remains in equilibrium locally while exhibiting the prescribed global average strain of s . In the HE fibers, peak strains, greater than - , occur in the fibers adjacent to the fragment tip, i.e., fiber 1 at x = 0. In the LE fragments, peak strains occur at the fragment mid-point, x = L. The peak strains in the LE fragments will be less than - since a significant fraction of the fragment’s total displacement generally arises through slip of the fragment tip.

Peak strains in the HE fibers and LE fragment are exhibited in Figures 5 and 6, respectively. For moderate to high values of Q, peak HE fiber strains are seen to be lower for hexagonal packing versus square packing, particularly for larger fragment sizes. At low values of Q, the regime where fricitional slippage effects dominate, peak HE fiber strains are the same for both packing schemes. LE fragment peak strains are higher for hexagonal as compared with square packing.

Taken together, the results for peak fiber/fragment strains and LE fragment load contribution suggest that blended fiber arrays with increased packing density provide improved mechanical performance in post-fragmentation yarn extension. The LE fragment provides better reinforcement of the fiber array in the more densely packed hexagonal configuration. Since more densely packed fiber arrays do not lead to higher peak strains in the HE fibers, increased packing density is not expected to reduce the rupture strain of the yarn and may increase it somewhat for moderate to high Q values. Higher peak LE fragment strains in the hexagonal versus square packed array suggest that the progressive fragmentation of the LE fragment will proceed at a higher rate in more densely packed arrays. Therefore, we expect at a given yarn extension, more densely packed fiber arrays will exhibit shorter mean LE fragment lengths (the fragments have experienced a greater number of successive breaks) than less densely packed arrays.
4. CONCLUSIONS
We have modified a simple model representing the microstructure of a blended yarn undergoing axial extension for the assumption of hexagonal fiber packing. The present results have been compared to previous results for the assumption of square packing. Through this comparison, it has been shown that increased packing density provides for better reinforcement of the yarn by the LE fragments. In addition, fiber strain results suggest that blended yarns having more densely packed microstructures are likely to exhibit somewhat higher strains to complete rupture than blended yarns with less densely packed microstructures.
Thomas A. Godfrey
US Army Soldier & Biological Chemical Command
Natick Soldier Center, Natick, MA 01760-5020
Email: Thomas.Godfrey@natick.army.mil
John N. Rossettos
Department of Mechanical, Industrial, and Manufacturing Engineering
Northeastern University, Boston, MA 02115
Email: jross@coe.neu.edu