Modeling of Yarn Hairiness

ABSTRACT:

Hairiness is defined as the sum of fiber ends and loops protruding out from the main compact yarn body. Beside other instruments, there are two major testing equipments available on the market used for evaluating the yarn hairiness. The most popular instrument is the Uster hairiness system, which characterizes the hairiness by H value, and is defined as the total length of all hairs within one centimeter of yarn. The hairiness H is an average value and giving no indication of the distribution of the length of hairs. Main aim of this contribution is to analyze the yarn hairiness distribution for compact yarns according to the possibility of fitting bimodal function; i.e. dividing the hairiness to two types of hairiness. The individual values of yarn hairiness were extracted fro Uster tester 4 and fed to a computer program HYARN written in Matlab code for complex characterization of yarn hairiness. The results show that in general, the fiber hair distribution has a bimodal shape and comprises a mixture of two Gaussian distributions. Also the data was used for complex evaluation of yarn hairiness in time and frequency domain.

1. INTRODUCTION

Yarn hairiness is a complex concept, which generally cannot be completely defined by a single figure. The hairiness occurs because some fiber ends protrude from the yarn body, some looped fibers are out from the yarn core and some wild fibers appear on the yarn surface. Hairiness of yarns has been discussed for many years, but it always remained a fuzzy subject. With the advent of compact yarns and their low hairiness compared to conventional yarns, the issue of measuring hairiness and the proper interpretation of the values has become important again. Generally speaking, long hairs are undesirable, while short hairs are desirable.

The effect of yarn hairiness on the textile operations following spinning, especially weaving and knitting, and its influence on the characteristics of the product obtained and on some fabric faults has led to the introduction of measurement of hairiness.

The most popular instrument for hairiness evaluation is the Uster hairiness system, which characterizes the hairiness by H value defined as the total length of all hairs within one centimeter of yarn. The hairiness H is an average value giving no indication of the distribution of the length of hairs. The spectrogram of hairiness is also available. The second major used instrument is the Zweigle hairiness tester. The numbers of hairs of different lengths are counted separately. In addition to the S3 value is given as the sum of the number of hairs 3 mm and longer. The information obtained from both systems is limited. The available methods compress the data into a single value (deletion of the important information about statistical behavior) or convert the entire data set into a spectrogram. Other methods dealing with image processing are time consuming.

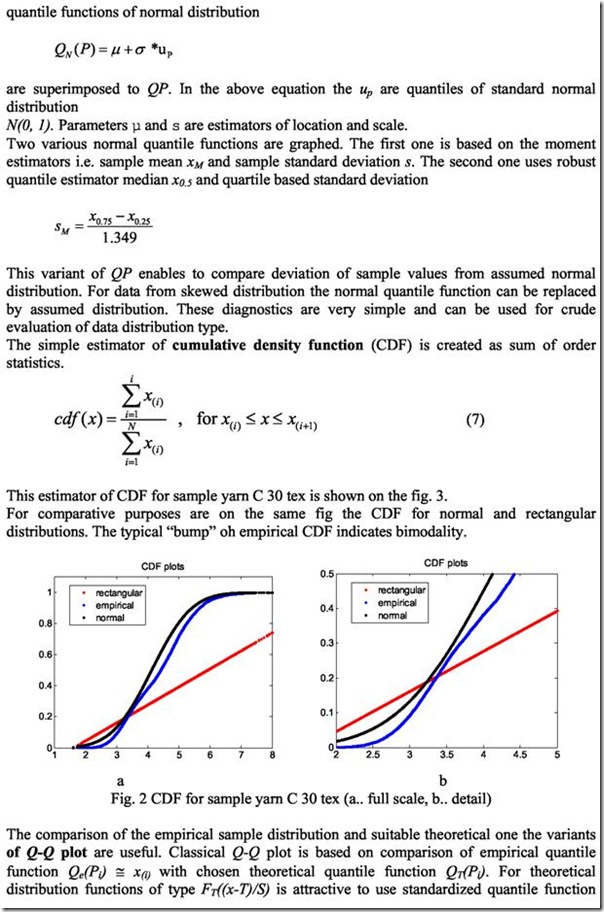
Modern USTER devices have possibility to give raw data about whole yarn hairiness in the length interval of hundreds meters. The raw data Hi are in fact realization of spatial process (hairiness spatial process - HSP) and can be used for more complex evaluation of hairiness characteristics in the space and frequency domain.

Main aim of this contribution is to identify the yarn hairiness distribution shape. The individual values of yarn hairiness (HSP curve) are extracted from Uster tester 4. The standard and special techniques of data visualization and uni-modality testing are shown. The simple methods for complex characterization of HSP statistical behavior (stationarity,

independence, linearity etc.) are presented. The computer program HYARN written in Matlab code is used for complex characterization of yarn hairiness stochastic behavior. Many as 45 yarns spun on different systems, namely classical Ring spun, compact, Siro spun, plied yarns, and vortex spun yarns were tested. The yarn counts was ranging between 14.6 to 30 tex. All yarns were cotton, except the vortex yarns, which was spun from viscose staple fibers. The results show that in general, the yarn hairiness distribution obeys a bimodal shape (short and long hairs) and can be described by a mixture of two Gaussian distributions.

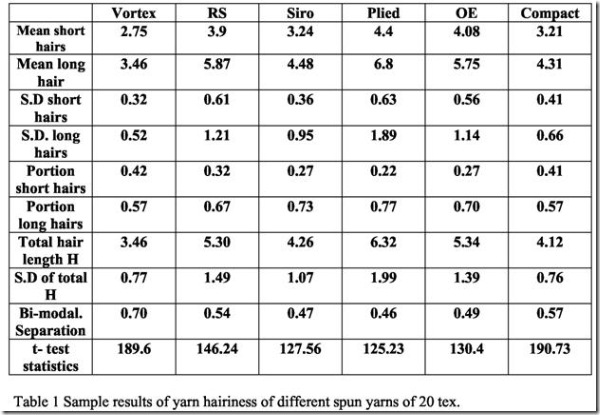
Table 1 shows the different values obtained from H-yarn program. It obvious that the lowest values for long hairs are due to vortex yarns followed by compact yarns and siro spun. The highest values are due to plied yarns. This may be due to the plied yarns passes more stages during processing. This result is also valid for the length of the long hairs and also for the total yarn hairiness H. The percentage of short fibers for both vortex and compact yarns are comparable and has the highest values. The standard deviation, which is a measure of the variation in yarn hairiness distribution for both components the short and long hairs, has the same trend.

6. YARN HAIRINESS AS A STOCHASTIC PROCESS:

The data extracted from Uster is taken in equidistance (time interval), so that it can be used for more complex evaluation of hairiness characteristics in the time and frequency domain. The yarn hairiness can be described according to the:

- Periodic components - Random variation

- Chaotic behavior

For these goals, it is possible to use system based on the characterization of long term and short-term dependence of variance. The so-called Hurst exponent or fractal dimension can describe especially long-term dependence. Here we shall deal with a limited functions from many characteristics computed in our H-Yarn Program. Details are found in [4].

As an example, the autocorrelation, which simply can be described as a comparison of a signal with itself as a function of time (distance) shift (lag) is illustrated in Figure (9).

Also, concerning frequency domain analysis, we demonstrate the FFT, which is also used for transforming time domain function into frequency domain and its inverse. The signal is decomposed to different sine waves. There are many types of spectrum, PSD, amplitude spectrum, and many other types. The power spectrum output from H-Yarn program is illustrated in figure (9). The cumulative of white identically distribution noise is known as Brownian motion or random walk. The Hurst exponent is a good estimator for measuring the fractal dimension. The Hurst equation is given by: R/S= K^*(N)^H. This can be seen in the same figure (last row).

7. CONCLUSIONS:

· The yarn hairiness distribution can be described by two Gaussian, the portion, mean and the standard deviation of each component leads to deeper understanding and evaluation of

hairiness.

· The Hyarn system is a powerful program for evaluation and analysis of yarn hairiness as a dynamic process, in both time and frequency domain.

· H-yarn program is capable of estimating the complexity of this process.

· Great deal of effort should be undertaken due to Zweigle system for evaluation of yarn hairiness.

· Comparing the results of different systems for yarn hairiness evaluation are of great help for industry.

Jiří Militký¹⁾, Sayed Ibrahim ²⁾ and Dana Křemenáková²⁾

¹⁾Dept. of Textile Materials, ²⁾ Dept. of Textile Technology, Technical University of
Liberec, 46117 Liberec, Czech Republic.

Acknowledgement: This work was supported by the research project 1M4674788501 - “Textile Center” of Czech Ministry of Education.