DETERMINATION OF TRANSFER FUNCTION FOR OE – ROTOR SPINNING SYSTEM

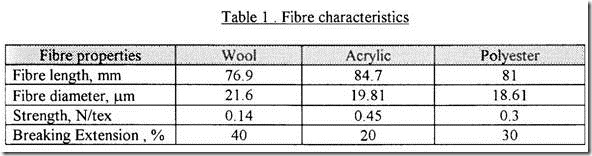
At present the significant direction of researches on the processes and systems of spinning technology is to find out a scientific method of dynamic simulation. This can be done by the application of the theory of random function. The principle lies on the conception of technological system as a stationary, linear dynamic system. The aim is to determine the modulus of the relative transfer function and subsequent technological analysis. The acts can be stated as to determine the influence of technological factors on the equalization effectiveness to a given spinning system and also to determine the conditions for improving the quality of the resulting linear fiber products (for example, sliver, roving, and yarn) from the point of view of mass irregularity.

It is necessary to point out that a procedure of dynamic simulation can solve the question of transformation through the spinning systems. The problem of transformation can also be solved with the help of determination of quadratic mass irregularity of short sections of the linear fiber products on the basis of autocorrelation function of mass irregularity.

Choice of the technological application of dynamic simulation

As an example of the method of dynamic simulation as well as process of determination of quadratic mass irregularity of short section of linear fiber product, we can discuss about the following technological applications.

- flat card with a drafting mechanism [ 1 ] – evaluation of the leveling effectiveness - a system of successive and combined doubling[2]- levelling effectiveness,

- the resulting quadratic unevenness, the technological causes of an increased levelling

effectiveness, the effect of replacement of spinning rotors with the increasing

frequency of revolution

- system of cyclic doubling [3] – the resulting quadratic unevenness, the influence of the collecting surface diameter of the rotor, requirements of the fiber flow taken over by the collecting surface

- the separating device of the OE- spinning system [4] – influence of the structure of the mass irregularity in the fiber flow

The main problem in the application of method of dynamic simulation is the process of determination of transfer function, subsequently modulus of relative transfer function. Relevant determination is possible with theoretical or experimental process. Dynamic model detailing transformation of mass irregularity comes from two basis aspects of a given technological problem. With these two basis aspects of the specified research problems, the following possibilities can be stated:

a) the quantities expressing the character of the characteristic property of a fiber product: these can be

- deterministic or

- random

b) the mechanical and physical action defining the character of the technological environment can be characterized as

- deterministic or

- random

In the dynamic model, the character of fiber product from point of view of mass of short sections of linear fiber product is random. The character of technological environment i.e., system of transformation is determined by the simplifying condition of processes.

Modulus of relative transfer function for OE – rotor spinning system

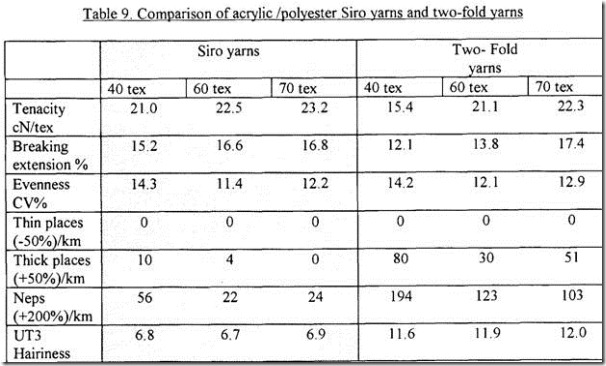
The concept of OE – rotor-spinning system as a dynamic system including the division into partial dynamic system is stated in [5]. An equation expressing the modulus of relative transfer function for system of cyclic doubling in spinning rotor process can be found in [5]. The main content of the present work is the presentation of results of experimental procedure for determination of the modulus of relative transfer function for OE – rotor-spinning system and the possibility of use of the apparatus Uster Tester 4 – SX is also explored. The spectrograms obtained from the above-mentioned apparatus may be directly used for determination of the modulus of relative transfer function for the given system. In principle, this acts about record harmonic components of mass irregularity depends on the wavelength. Instead of amplitude of the harmonic components, the quadratic mass irregularity (CV) of the harmonics components is plotted along the y-axis. This is directly proportion to the relative amplitude, so the modulus of the relative transfer function can be directly expressed as a ratio between the CV values of the corresponding harmonic components. It is important to obtain the CV values correctly in order to obtain correct values of the modulus, hence efficient application.

Results of experimental determination of the modulus of relative transfer function for the OE–rotor-spinning system are given below.

Interpretation of results and conclusion

The method of determination of the modulus of the relative transfer function for a given spinning system with the use of spectrograms obtained from the apparatus Uster Tester 4-SX makes it possible to obtain a function that characterizes transformation of the structural mass irregularity of the input fiber product (sliver) on the structural mass irregularity of the resulting or output fiber product (yarn). It offers a picture on the components of the OE-spinning system, which is important for preparation of sliver with optimal structural mass irregularity.

In the given example of OE-rotor-spinning system, it is known that there exits two very contradictory effects from point of view of mass irregularity, that is, the opening system highly increases the mass irregularity and the cyclic doubling reduces it. Globally,

the OE-rotor-spinning system is known as a system of very high draft (in the given example draft is P = 236) and that matches with the resulting modulus of the relative transfer function. It is evident, that with reference to the very high draft, given to an OE-rotor spinning system, thanks to the system of cyclic doubling, that decreases the mass irregularity!

A new philosophy, which uses the principle of dynamic simulation opens new directions of research for analysis of structural mass irregularity with a view to different consequential optimization of different spinning systems from the point of view of mass irregularity of the resulting fiber product.

P.Ursíny,R.K.Nag

Department of Textile Mechanical Technologies, Faculty of Textiles,
Technical University of Liberec, Hálkova 6, Liberec 1, 461 17, Czech Republic

Read more...

Siro And Two-Fold Yarns

Investigation was carried out on how the tensile and related properties of Siro yarns, spun from two separated rovings of different types of materials, were affected by the twist factor and draft. Comparison on Siro yarns and two-fold yarns of the same linear density and twist factor revealed that the former was better in tensile strength and related properties. The Siro yarns are believed to be able to bear extra tension during manufacturing processes such as weaving and knitting.

Keywords : yarn strength, evenness, imperfections, hairiness.

1. INTRODUCTION

In Siro spinning, two parallel fibre strands, separated at a distance, are drafted simultaneously in the drafting zone. After they emerge from the front roller nip, they converge to form a yarn by twisting. Previous researches"⁾ mostly focused on studying spinning geometry and yarn parameters for producing yarn from rovings of the same fibre type. There has been very limited information available regarding the use of rovings of two different kinds of materials on the Siro system. Thus, the present work was designed to carry out some spinning trials on attenuating two rovings of different fibre materials in the drafting zone and to investigate the capability of the resulting Siro yarn.

In staple yarns, twist is essential to hold the fibres together and to impart some degree of cohesiveness to the structure. Twist is a means by which a bundle of fibres is held together so that the ultimate structure is made capable of withstanding the stresses and strains generated in the next manufacturing steps. The role of twist in yarn is essential to manipulate the yarn properties. Thus, the influence of twist on the Siro spun yarn tensile strength was also included in the present work.

2. EXPERIMENTATION 2.1. Selection of materials

Wool, polyester and acrylic fibres were selected for the study. The characteristics of the fibres are shown in Table 1. All samples prepared for the present work were conditioned and tested under standard atmospheric conditions ( 20 + 2°C and 65 ±2 % relative humidity).

The Instruments for testing the fibre properties are listed in Table 2. The processing parameter used in drawing and roving are shown in Table 3. Table 4 gives the sequence of machinery used to produce the yarns.

2.2. Production of two-fold yarn

Comparison was made between Siro and two-fold yarns of the same linear density. A worsted twist factor of 2.2 [2600 (tpm x ^-qtex)] was adopted. This enabled the advantages of Siro yarn to be compared with those of two-fold yarn. Comparison was also made between the yarns of different linear density, to identify the effect of changes in draft on the properties of the two series of yarns.

Since the folded twist of the two-ply yarn should be equal to that of its corresponding Siro yarn, and the folded twist of a two-ply yarn is usually set at 70% of that of the single yarn, it is necessary to calculate the required twist that should be inserted into the single yarn by dividing the folded twist by 70%. Table 5 shows the required amount of twist inserted into the yarns.

3. RESULTS

The properties of the Siro and two-fold yarns are compared in Tables 6-9. 3.1. Comparison and•evaluation amongst Siro and two-fold yarns

Referring to Table 6, for pure wool worsted yarns, when the yarn linear density increased from 40 tex to 70 tex, the tenacity of the two-fold yarns increased from 7.8 to 8.3 cN/tex while that of the Siro yarns increased from 6.7 cN/tex at 40 tex, 8.5 at 60 tex to 8.7 at 70 tex. The Siro yarns, except for the 40 tex, were significantly stronger than the two-fold yarns, by 4.7% to 14.9% at twist factor 2.2. The breaking extension of Siro yarns was also significantly better than that of the two-fold yarns, by 60% to 73%. The evenness of the two-fold yarns was better than that of Siro yarns. At the twist factor of 2.2, Siro yarns were significantly less hairy than the two-fold yarns, by 10% to 18%.

For the wool/acrylic blended yarns, in referring to Table 7, the tenacity of two-fold yarns increased from 9.7 cN/tex at 40 tex, to 11.0 at 60 tex and 11.6 at 70 tex. Tenacity of the Siro yarns increased from 13.3 to 15.4 cN/tex. The Siro yarns were significantly stronger than the two-fold yarns, by 32% to 37%. The breaking extension of the Siro yarns was higher than that of two-fold yarns, by 56% to 125%. The evenness of the Siro yarns was better than that of two-fold yarns. The yarn evenness CV% of the two-fold yarn ranged from 15.8 at 40 tex to 13.1 at 70 tex while the evenness CV% of the Siro yarns decreased from 15.5 to 11.9 as the yarn linear density increased. The hairiness of the Siro yarn was lower than that of the two­fold yarn, by 44% to 50%.

From Table 8, it can be seen that the tenacity of wool/polyester Siro yarn was higher than that of the two-fold yarn, by 6% to 23%. The tenacity of the two-fold yarns increased from 13.9 cN/tex at 40 tex, 14.9 at 60 tex to 15.8 at 70 tex. The tenacity of Siro yarns increased sharply from 14.8 to 19.5 cN/tex. The breaking extension of the Siro yarns was higher than that of the two-fold yarns, by 3% to 20%. The evenness of the Siro yarns was also better than that of the two-fold yarns. The evenness of the Siro yarns and two-fold yarns ranged from 17.6 at 40 tex to 12.6 at 70 tex and from 18.6 at 40 tex to 13.9 at 70 tex, respectively. The Siro yarns were significantly less hairy than the two-fold yarns, by from 30% to 41%.

For the synthetic (acrylic/polyester) fibre blended yarns (Table 9), the tenacity of the two-fold yarns increased sharply from 15.4 to 22.3 cN/tex as the linear density increased from 40 tex to 70 tex. The Siro yarn again exhibited better tensile strength, by 4% to 27%, compared to the two-fold yarns; it increased from 21.0 cN/tex at 40 tex, 22.5 at 60 tex to 23.2 at 70 tex. The breaking extension was generally higher for the Siro yarns. The evenness CV% of the Siro yarns decreased from 14.3 to 12.2, and that of the two-fold yarns decreased from 14.2 to 12.9, as the yarn linear density increased. The two-fold yarns were more hairy than the Siro yarns. The hairiness of the two-fold yarns increased from 11.6 to 12.0 and the hairiness of the Siro yarns increased from 6.8 to 6.9 as the linear density increased from 40 tex to 70 tex.

4. DISCUSSION

The present work focused on a comparison of the yarn properties of Siro yarns and two-fold yarns of equivalent yarn linear density. It was found that the Siro yarns were generally superior to the two-fold yarns in terms of yarn strength.

The breaking strength of the Siro yarn is higher than that of the two-fold yarns of equivalent linear density due to the particular Siro yarn structure - due to the fibres being more firmly bound within the yarn structure. The two twisted strands of the drafted fibres caused some surfaces fibres to be trapped into the Siro yarn so as to increase the inter-fibre cohesion in the yarn which can withstand higher breaking forces. In Siro spinning, the sense of twist is the same for both the single ends and the composite product. This gives a yarn that is somewhat more compact , with a firmer core, than the usual two-fold yarn with opposing singles and folding.

The better tenacity of Siro yarn could also be ascribed to the fact that the single strands have comparatively low twist which results in better and more even load sharing by the constituent fibres. In the process of yarn formation, fibres distribution is subjected to the twisting operation. The combination of varying numbers of fibres per cross section with varying forces binding these fibres together because of twist variation leads to varying tensile properties.

Another relevant factor with respect to the inferior yarn strength of two-fold yarns is the additional freedom of lateral movement permitted to the fibres. During extension of the yarn, the plies become grossly deformed r.nd the lateral displacement of fibres at different initial positions appear to follow a complex pattern. Fibres initially in the centre of the plies begin to move towards the central yarn axis. Fibres at greater initial radial positions in the plies simultaneously begin to gather around their own ply axis which is already moving independently towards the yarn axis.

The Siro yarns generally also performed better than the two-fold yarns in terms of evenness and degrees of imperfections. This is because the Siro yarn is produced by two strands of roving ; there would be a better parallel and straightening effect between the separated fibre strands during drafting. Since peripheral distribution of fibres during spinning is a combined effect governed to a large extent by the staple length, fibre cross-sectional resistance to twisting and other process parameters, it would not be possible to deduce the exact relationship of the combined fibre parameters and yarn unevenness. The poorer uniformity of the two-fold yarns may also be due to the greater number of production processes involved in producing two-fold yarns as compared to Siro yarns.

K.P.S. Cheng & C.H. Yuen

Institute of Textiles and Clothing, The Hong Kong Polytechnic University

Read more...

CONTROL OF LAP AND CARD SLIVER EVENNESS AND CARD WEB NEPS WITH MECHANICAL VARIABLES AT SCUTCHER

 

Different setting points of scutcher i.e. feed roller to krischner beater, krischner beater to stripping rail and grid bar gauges
were changed and their effect on lap evenness, card sliver evenness, and card sliver neps was observed. It was noted that feed
roller to krischner beater and krischner beater to stripping rail for evenness and all the setting points for sliver neps showed

highly significant differences in the mean values for different settings. Key words: lap evenness, scutcher settings, sliver evenness

INTRODUCTION

Cotton delivered by the opening machinery to the scutcher is well opened and usually arrives in the form of large tufts. Scutching is a process of cleaning by striking the cotton from a pair of rolls to a rapidly revolving beater after which it is formed into a continuous sheet of small tufts of cotton, held together by compression. The objectives of the scutching operation are: first, to continue the opening of the cotton even further than has already been done; second, to clean the cotton of more of the heavier dirt and undesirable short fibres; third, to form this cleaned cotton into a continuous sheet called a "Lap"; and fourth to make this lap as uniform as possible. The scutcher section may be classified as: feed unit, beater section, screen section and lap head. With improvements in trash extraction at earlier stages of processing, the extraction of trash at scutcher has been of less importance than making a uniform well textured lap. Khan (1972) found that regularity of sliver is dependent upon the uniformity of scutcher lap. Shrigley (1973) reported that incorrect setting of stripping rail is detrimental to lap regularity. Ratnam and Seshan (1987) mentioned that the short term variation in card sliver contributes 3.2% of the total, provided the sliver is regular. Variation introduced by cards together with the variation in blow room, a major part of this variation, can be attributed to blow room. Almashouley (1988), reported that inadequate settings and inadequate feedings are the sources of variation in weight per yard of lap. Alan and Alexander (1988) pointed out that processing of fibres tends to produce neps through a stress build up/sudden release mechanism which induced buckling along the fibre length. Ali (1998) reported that calender rolls pressure. kirschner beater gauges and kirschner beater speed mainly influenced the lap weight variation. He also recommended that CV of meter to meter lap weight be strictly controlled and maintained at level less than 2%. Anonymous (1999) recommended that distance between stripping rail and the kirschner beater should be 2mm. In case. distance between rail and beater is greater, this will badly influence flow of material and cause soft lap. Robert e at. (2000) observed that considerable amounts of short fibre content. created in production and processing, are removed

in the combing process. This study was undertaken to determine the effect of different setting points of scutcher on lap and card sliver evenness and card sliver neps.

MATERIALS AND METHODS

Lint cotton samples of Punjab American cotton variety MNH-93 were collected from the running material at M/S Nishat Mills Ltd., Faisalabad. The raw cotton samples were subjected to following physical tests:

Spinning Procedure: The samples were processed at Ohara
Hergath blow room line (Model 1988) with the following

changes at scutcher in blow room.

i. Feed roller to kirschner beater gauge: F1 =3 mm, F2=5 mm, F3= 7 mm

ii. Kirschner beater to stripping rail gauge: S,=2 mm.

S2=3 mm, S3=4 mm

iii. Kirschner beater grid bar gauge: G1=5 mm, G2= 7 mm,

G3= 9 mm

After every change at scuther, the samples from laps were collected and tested for the basic fibre characteristics along with the following lap quality evaluation tests:

Lap Evenness: This is yard to yard weight variation of lap and was determined by cutting it into one yard pieces then weighing each piece in grams on the weighing scale and in this way the coefficient of variation was calculated.

Sliver Evenness: Sliver evenness (U%) was determined on Uster Tester-llI according to the procedure supplied by the manufacturer, M/S Zellweger Ltd. (1995b). Uster Tester speed was set at 25 meter per minute for each test.

Card Web Neps: Neps were counted by AFIS-N according to the instructions laid down in its operational manual supplied by M/S Zellweger Ltd. (1992), Switzerland.

Three factor factorial completely randomized design was applied for testing differences among various quality characters evaluated in this study. Duncan's multiple range test was applied for individual comparison of means among various quality characteristics as suggested by Steel and Torrie (1980). The data were subjected to statistical manipulation on computer employing M-Stat computer programme designed by Freed (1992).

RESULTS AND DISCUSSION

Lap Evenness :The results pertaining to lap evenness are
shown in Table I. This Table shows that the effect of feed

roller to beater gauges, beater to stripping rail gauges and interaction F x S generate highly significant differences among mean values. The results in respect of SxG interaction also showed significant differences, while the effect of rest of gauge and interactions on lap evenness was non-significant.

The individual mean values of lap evenness recorded the best value as 0.80% at F2 followed by 0.87 and 0.93% for F3 and FI respectively while these gauges significantly differed in their mean values. Above results show that the setting F2 gives minimum lap. Similar views are given by Almashouley (1988), who reported that inadequate settings and inadequate feedings are the sources of variation in weight per yard of lap, while Ali (1998) reported that ealender rolls pressure, kirschner beater gauges and kirschner beater speed mainly influenced the lap weight variation. He also recommended that CV of meter to meter lap weight be strictly controlled and maintained at level less than 2%.

The comparison of individual means for beater to stripping rail gauges recorded the best value of 0.65% CV for SI followed by 0.85 and 1.10 % S2 and S3 respectively and recorded significant differences between the individual means. These results coincide with those of Anonymous (1999) which recommended that distance between stripping rail and the kirschner beater should be 2mm. In case, distance between rail and beater is greater, this will badly influence flow of material and cause soft lap. Likewise Shrigley (1973) reported that incorrect setting of stripping rail is detrimental to lap regularity. In case of grid bar gauges, the order for grid bar settings G3, G2 and G I was recorded as 0.85. 0.87 and 0.88 % respectively. These results indicated that the means of grid bar gauges recorded non­significant differences with respect to individual means. Sliver Evenness: The results pertaining to the sliver evenness are given in Table 2. This Table showed that the effect of feed roll to beater gauges, beater to stripping rail gauges and interaction F x S was highly significant. However, grid bar gauges and remaining interactioris were found to have non-significant effect. The individual mean values for sliver evenness between feed roller to beater gauges were recorded as 3.88, 4.12 and 4.28 % for F2, F3 and F1 respectively. Present results indicated significant differences among the individual means. These results are in line with those of Khan (1972) who found that regularity of sliver is dependent upon the uniformity of scutcher lap, while Ratnam and Seshan (1987) stated that the short term variation in card sliver contributed 3.2% of the total, provided the sliver is regular. Variation introduced by cards is in addition to the major variation caused in blow room. The comparison of individual mean values for beater to stripping rail gauges is shown in Table I. The best value of sliver evenness (3.31%) for SI was followed by S2 and S3 with respective means of 4.17 and 4.80%. These values showed significant differences among individual means indicating that the close gauge SI gave the best results for lap uniformity than for sliver uniformity, since the variation in lap leads to the variation in card sliver. These results get support from Merill (1960) who recommended that the stripping rail must be close enough to beater. Shrigley (1973) reported that incorrect setting of stripping rail is

detrimental to lap regularity. Khan (1972) found that regularity of sliver is dependent upon the uniformity of scutcher lap.

Comparison of individual means for grid bar gauges are shown in Table 2a. The individual mean values for grid bar gauges were 4.05, 4.10 and 4.13 % for G" G1 and G2 respectively, indicating that there was no effect of grid bar gauges on the regularity of card sliver.

Card Web Neps: The results pertaining to card web neps for different settings at scutcher in blow room are shown in Table 3. The results revealed that the effect of feed roller to beater gauges, beater to stripping rail gauges. grid bar gauges and interactions F x Sand S x G are highly significant, while interactions F x G and F x S x G differed significantly.

Duncan's multiple range test for comparison of individual means of card web neps for feed roller to beater gauges are shown in Table 1. The minimum web neps are recorded at F2 followed by F3 and F1 with their respective means as 80.17, 88.03 and 94.08 neps per gram. These results indicated that close gauge produced more fibre breakage and neps. Similar were the findings of Wegener (1980) who reported that neps originated from growth, harvesting, ginning, and processing and are often formed form fibre breakage. causing the fibre to coil itself, thus involving other fibres in its recoiling and producing entanglements. Similarly, Dever et at (1988) observed that neps are formed by increased aggressive cleaning. However. Alon and Alexander (1978) pointed out that processing of fibres tends to produce neps through a stress build up/sudden release mechanism which induces buckling along the fibre length.

The comparison of individual means for beater to stripping rail, gauges generated the minimum number of neps for SI followed by S2 and S3 as 69.69,88.94 and 103.65 neps per gram respectively. However, the individual means significantly differed from each other. These findings are supported by Shrigley (1973) who found that the stripping rail setting is the most important, since a setting that is too wide may permit the cotton to pass around with the beater instead of being discharged, thereby creating neps and flocking, whereas Steadman (1997) reported that neps seldom appear in boil, but every processing stage has the potential to be susceptible to fibre aggregation. When properly managed, both carding and combing can remove more neps than generated.

In case of grid bar gauges, the minimum number of neps was recorded at G3 followed by G2 and G I with their respective mean values as 85.11, 87.36 and 89.81 neps per gram. indicating significant differences between the individual means. More opening of grid bars generates more cleaning and less neps. Sheikh (1997) reported that an increase in seed, trash particles in cotton is associated with higher nep content. Herbert et at (1986) observed that three types of neps are present in cotton: i) entanglement with seed coat fragment, ii) entanglement with trash, and iii) non-fibrous material entanglement, while Harrison and Barge/on (1986) observed that neps are important in determining the quality of final product of cotton fabrics. Fibre characteristics and processing conditions are two factors that affect the nep formation.

Conclusion: The study showed that too wide stripping rail

setting with the beater may permit the cotton to pass round and round with the beater instead of being discharged which damages the fibres and generates neps, thus the rail must be close enough for proper functioning.

Read more...

Magnetic Ring-Spinning Revolutionizing the Tradition

In today’s spinning technology, at least 4 types of spinning systems are commercially available. These are the tradi­tional ring spinning, rotor spinning, airjet spinning and friction spinning. Among them, ring spinning stands alone in providing high quality yarn suitable for any type of tex­tile end product. Other more recent systems enjoy much higher production speed than traditional ring spinning, but yarn quality restricts their use to only narrow ranges of tex­tile products. The primary technological limitation of ring spinning lies in the speed of the ring-traveler system. The traveler is a C-shaped thin piece of metal that is used for a limited period of time, disposed, and replaced on frequent basis. Three specific issues must be addressed to overcome this limitation:

· the dependence of the yarn linear speed (or delivery speed) on the rotational speed of the traveler

· the continuous need to stabilize yarn tension during spinning and the dependence of this stability on the traveler speed

· the impact of traveler speed on fiber behavior in the spinning triangle

Research to date has only provided about a 15% improve­ment in traveler speed without affecting the traveler/ring contact thermal load capacity. Ring spinning is still at a production rate disadvantage of 15 to 20 times in compari­son with other spinning systems. Therefore, the challeng­ing issue is how to break the traditional paradigm of ring spinning and revolutionize its principle in such a way that very high speed can be achieved without sacrificing the tra­ditional quality of ring spun yarns.

Our design approach is to totally eliminate the traveler from the ring spinning system and replacing it with a mag­netically suspended lightweight annular disc that rotates in a carefully pre-defined magnetic field (See Figure below). By creating a non-touching environment of the rotating element for ring spinning this system provides a super high spinning rotation without the limitations of the current trav­eler system.

Finite element system simulation

We are simulating the magnetic system using a magnetic finite element package. The magnetic field strength distri­bution on different system components shows the support­ing forces exerted on the rotor part (See Figure below).

Our first estimate is that these forces are 25 N in the radial direction and 15 N in the axial direction. We are seeking more axial stiffness of the rotor.

Contributing Graduate Students: Gangumalla Yamshi Reddy, Jayendra S. Dabahde (Auburn).

Industry Interactions: 2 [Unifi, Velcro] Academic non-NTC Interactions: 2

Project Web Address: http://www.eng.auburn.edu/~fhady/magnetic-report.htm

Faissal Abdel-Hady, a Research Assis­tant Professor of Textile Engineering at Auburn since 1998 and an Assistant Professor of Mechanical Engineering at Ain Shams (Egypt), earned a B.S in 1975 and M. S. in 1981 there and a Ph.D. in 1988 at Ecole Nationale Superieure des Mines de Saint Etienne (France), all in mechanical engineering. Faissal then was a manager in industrial soft­ware for Hicon France. His research interests include thermal analysis. stress simulation, automatic control and mechatronics, mechanical compo­nents, CAD/CAM for filament wound structures, dynamic signal processing and software development.

S00-AE06, F01 -AE02*, S01 -AE32 fhady@eng.auburn.edu

(334)-844-5471 http://www.eng.auburn.edu/~fhady

By replacing the traveler in ring spinning
with a disc that rotates in a magnetic field,
we hope to maintain
the high quality of ring spun yarn,
but at much higher speeds.

Read more...

EFFECT OF BLENDING RATIOS AND TECHNIQUES ON THE QUALITY PARAMETERS OF 30'S POLYESTER/COTTON YARN

The present study was conducted to determine the impact of polyester/cotton ratio on the quality characteristics of yarn. The quality characters depend upon the ratio of polyester and cotton in the blend and also on the blending technique adopted during fibre production to yarn spinning. The quality characters such as single yarn strength, yarn elongation and rupture per kilometer of yarn were directly proportional to the ratio of polyester with cotton in the blend. Draw frame blending produced better quality yarn as compared to blow room blending, lap former blending and simplex blending.

Keywords: blending techniques; cotton/polyester ratio

INTRODUCTION

The cotton has a loin's share in the economy of Pakistan. It provides raw material for our leading industrial sector. The growing world population needs and ever-changing fashions have changed the consumer trends. Now they demand great versatility, wide variety, higher standards and precision in fabrics, which are scarce in cotton products due to fibre to fibre variation, pest attack and uncontrollable environmental conditions. Therefore, the natural fibres are blended with synthetic fibres, such as cotton with polyester. The ratio of natural and synthetic fibres in the blend is of prime importance due to its multiple uses, economical and environmental conditions. Blending of natural and synthetic fibres is still carried out in sliver form on the draw frame (Klein, 1987). This provides the best blend in the longitudinal direction. Nawaz et al. (1999) reported that there is a gradual decline in yarn strength as the share of polyester fibres decreases in the blend. Li and Van (1990) reported that fibre properties had a significant effect on yarn strength. Anandjiwal and Goswami (1999) investigated that the blending of dissimilar fibres leads to their non-uniform distribution throughout the yarn cross-section, which in turn leads to preferential migration depending on both fibre properties and mechanism of certain spinning processes. The present study was conducted in order to find out the impact of polyester/cotton ratio on the quality characteristics of yarn and also to find out the optimal blending stage that produced excellent quality yarn.

MATERIALS AND METHODS

The present study on the comparison of different blending techniques of cotton and polyester at different stages during fibre to yarn spinning was carried out at the Kohinoor Textile Mills Ltd., Faisalabad and in the Department of Fibre Technology, University of Agriculture, Faisalabad during 1999-2000. Lint cotton samples of MNH-93 were taken from the mills, with

average values of fibre properties as fibre length 27.07 mm, fibre length uniformity ratio 48.58%. fibre bundle strength 90.81 thousand lb/irr', fibre fineness 4.52 ug/in, fibre maturity 82.53% and trash contents! 0.20%, while polyester fibre having the quality characteristics as fibre length 38 mm, fibre denier 1.2, colour/luster semidull, moisture regain 5%, elongation 18.30%, tenacity 7.04 glden and crimps per inch 13. 10, was used in the study.

The blendings of polyester and cotton were carried out in ratios i.e. RI (65:35) and R2 (52:48) at various stages i.e. blow room (TI), lap former (T2), draw frame (T3) and simplex frame (T4). The yarn thus prepared was tested for evaluation of following characteristics:

Tensile Properties of Single Yarn: The tensile properties viz. single yarn strength, elongation and rupture per kilometer, were calculated with Uster Tensorapid. The procedure adopted is that of ASTM Committee (1997). The data were analysed statistically using completely randomised design and Duncan's new multiple range test, as suggested by Steel and Torrie (1984).

RESULTS AND DISCUSSION

Single Yarn Strength: The statistical analysis of single yarn strength at 30' (P/C) blend is shown in Table I(a) which shows that the effect of different blending ratios and blending techniques during fibre to yarn spinning were highly significant, while the interaction between RxT on single yarn strength was non-significant.

The Table I(b) shows that the mean values of single yarn strength for 30' (P/C) yarn were observed as 412.45, 398.61, 422.03 and 387.38 g for TI, T2, T3 and T4 respectively. The best single yarn strength was noted in case of blending technique at draw frame while the lowest value was observed for simplex frame.

For blending ratio, RI (65:35 PlC) produced yarn of the best single yarn strength while the lowest value was in case of R2 (52:48 PlC) yarn. The results showed that more the percentage of polyester fibres, more would be the single yam strength and vice versa. Similar views were expressed by Nawaz et al. (1999) who reported a gradual decline in yam strength due to a reduction in polyester fibres in the blend.

Booth (1983) reported that several factors tended to influence the single yarn strength. He further reported that fineness of fibre affected several properties of the yarn and therefore, influenced the behaviour and properties of resultant yarn and fabrics. Hamid (1987) noted that the single yarn strength gradually diminished with a progressive increase in yarn number.

Yarn Elongation: The statistical analysis of yam

elongation at 30' (PlC) blend is shown in Table l(a) which showed that the effect of different blending ratios and blending techniques during fibre to yam spinning was highly significant while the RxT interaction on yam elongation value was significant.

The Table I(b) shows that the mean values of yam elongation for 30' (PlC) yam were observed as 8.04, 7.87, 8.08 and 7.71% for rt, T2, T3 and T4 respectively. The best yarn elongation was noted in case of blending at draw frame while the lowest value was observed for simplex frame. These findings were identical to those of Klien (1987) who found that blending of natural and synthetic fibres is still carried out in sliver form on the draw frame . This provides the best blend in the longitudinal direction. Regarding blending ratios, RI (65:35 PlC) produced yarn of best elongation while the lowest was obtained in case of R2 (52:48 PlC). These, results showed that the higher the percentage of polyester fibres, more would be the yarn elongation and vice versa. Elongation is a key factor (Sheikh, 1991). He further opined that the yarn elasticity and elongation were also very important in yarn spinning processes. Yarn with low elasticity i.e. Iow elongation tended to break more frequently in weaving. However, Zhu and Ethridge (1997) claimed that increase in elongation would reduce the hairiness of yarn.

Rupture per Kilometer of Yarn: The statistical analysis of rupture per kilometer at 30' (PlC) blend is shown in Table I(a) which indicates that the effect of different blending ratios and blending techniques during fibre to yarn spinning was highly significant while the RxT interaction on rupture per kilometer of yarn was non­significant.

Table I(b) shows that the mean values of rupture per kilometer for 30' (PlC) yarn were observed as 21.07, 20.48, 21.52 and 20.01 gltex for TI, T2, T3 and T4 respectively. The best rupture per kilometer of yarn was noted in case of blending technique at draw frame, while the lowest value was observed for simplex frame. These findings were similar to those of Klein (1987) who found that with evidently different raw materials (e.g. blends of natural and synthetic fibres), the blending at blow room was often unsatisfactory owing to uncontrolled extraction of flocks and the danger of subsequent de-blending.

As to the blending ratio, RI (65:35 PlC) produced yam of the best rupture per kilometer while the lowest was in case of R2 (52:48 PlC) yarn. The results showed that higher the percentage of polyester fibres, the more would be the rupture per kilometer of yam and vice versa. The properties of raw material seemed to directly influence the yam properties as reported by Li and Yan (1990) who remarked that fibre properties had a significant effect on yarn strength. However, Anandjiwal and Goswami (1999) investigated the blending of dissimilar fibres, leading to their disuniform distribution throughout the yam cross-section, which in turn led to preferential migration depending on both fibre properties and mechanism of certain spinning processes.

Conclusion: The study reveals that the quality characters such as single yarn strength, yarn elongation and rupture per kilometer of yarn were directly proportional to the ratio of polyester with cotton in the blend. However, draw frame blending produced better quality yarn as compared to blow room blending, lap former blending and simplex blending.

 

Shahid Saleem Shad^l, Asim Mumtaz¹ &. Iqbal Javed²
Departments of Fibre Technology' and Math. & Stat.", University of Agriculture, Faislabad

Read more...

The raw materials | The textile fibres

As known, the range of the textile fibres available on the market is at present rather extended. It includes in fact both natural and man-made fibres, which last were created about 100 years ago to the end of making up for the increased demand deriving both from the progressive improvement in the living standard and from the considerable growth of world population.

The natural fibres are divided, according to their origin, into animal (silk, wool, etc.) and vegetable (cotton, flax jute, etc.) fibres. Man-made fibres are divided into artificial (mostly originating from cellulose) and synthetic (from synthesis products) fibres.

In 1998 the world production of textile fibres amounted to over 47 million tons, which means a (potential) per capita consumption of about 8 kilos per year.

After the severe downturn of the world economy in the years 1992-93, in 1994 there was a recovery in textile production and consumption which went on, even if not at such a bright pace, also in the subsequent two years.

While cotton production depends substantially on the climatic conditions of the major producer countries and is therefore subject to heavy fluctuations (even up to 10%), the wool production is by now more or less stable since several years.

On the contrary the production of synthetic fibres, which in 1993 exceeded for the first time that of cotton, continued to grow, even if at a lower rate, in the following years to the extent that the synthetic fibre production exceeds nowadays that of the other fibres altogether.

Finally, as far as the production of artificial fibres is concerned, this is since some years slowly but steadily decreasing and accounts at present for only 4,6% of the global world fibre production.

Read more...

Cotton | A millenary history

All varieties of cotton (botanical name ″Gossypium″) grew originally in the desert zones of both the old and the new world. The cotton fibre was used probably at the end of the stone age in both hemispheres, to manufacture strings and maybe also fishing nets.

The time at which the real cotton growing started is not known, but from the remnants found at Cuzco (Peru) it was deduced that cotton spinning and dyeing date back to at least 2500 years ago; the excavations carried out in the village of Mohen Daro (Pakistan) gave evidence that cotton spinning and weaving were known already in 3000 B.C. Other archaeological finds prove that the Aztecs in Mexico and the Olmecs in central America, beside the Incas and their ancestors in the Andes produced cotton fabrics with very nice and complex designs which date back to over 2000 years ago.

The word ″cotton″ comes from the Arabic ″Katun″ which means plant of the conquered lands, with reference to the invasion of India by Alexander the Great in 327 BC. Several cotton fabrics still today bear the names of Asiatic and European towns, as well as of sea harbours situated along the cotton sea routes to Europe. Thus e.g. the term ″satin″ originates from the Arab name of the Chinese town Tseutung (Canton, today), the very popular ″denim″ from the French town Nimes, the name ″poplin″ from the papal city of Avignon and the name ″lisle″ from the French town Lille.

The cotton plant, as it originates from the desert, needs much sunlight and a warm climate; consequently it cannot be grown in Western Europe, except for Greece and Spain.

Production and consumption

The major cotton producing countries are at present China, the United States (the renowned ″cotton belt″ where the celebrated ″U.S. Upland″ cotton is being produced embracing several States: Texas, California, Mississippi, Louisiana, Alabama, Arizona and New Mexico), followed by CIS, India and Pakistan. According to a recent report of I.C.A.C. (International Cotton Advisory Committee), the world production of raw cotton in the harvest 1998-99 is estimated at around 18,3 million tons, recording a drop against previous years, while world consumption is predicted to remain at about 19,3 million tons (a rather stabile value).

The main exporting countries of raw cotton are the USA and the CIS (in the first place the state of Uzbekistan, followed by Turkmenistan and Tajikistan).

Cotton is mostly imported by those countries which, although having no possibility to grow it, have within their borders a more or less well developed textile industry. Typical countries are Italy, which in the biennium 1998-99 imported 355.000 tons of cotton, Germany (135.000 tons) and Portugal (174.000 tons). Russia too is a big cotton importer.

The major raw cotton producer countries (1997-1998 harvest)

In the Far East, the major raw cotton importer countries are Japan (278,000 tons, again in the year 1998-99), South Korea (275,000 tons), Thailand (315,000 tons) and Indonesia (386,000 tons). Even China imported about 400.000 tons of cotton.

These figures correspond in most cases to the consumption volumes.

Read more...

The cotton plant | Fibre characteristics

In ancient times the cotton plant was a perennial big shrub which bore fruits at all seasons; in time and after careful selections, almost in every country it has become a more or less branched out plant which is sown every year, grows and crops in 5 to 6 months.

The blooming takes place eight weeks after sowing, after few days the white and yellow flowers fall, leaving the boll which contains the seeds, around which the fibre fluff develops. In the subsequent weeks the capsule boll grows up to the size of a hen egg and bursts, releasing the white and bright cotton fibre which will continue to ripen until the harvesting time.

The cotton fluffs are picked either mechanically or manually and brought to the ginning room, where special machines called ″gins″ complete the separation of the fibres from the seed. The fibre mass is tightly compressed into bales, hence the term ″raw cotton″ used for this fibre. At this point the seeds are separated from the shorter cotton fibrils named ″linters″, which are used for the production of valuable artificial fibres, as we shall see later on.

From the botanical point of view, there are four basic species of cotton: Gossypium arboreum, herbaceum, hirsutum and barbadense. The first two species yield short staple, the third medium staple and the fourth long and extralong staple cottons (the term ″staple″ identifies the fibre length). In this connection we have to remind the prestigious varieties called ELS (extra-long staple), which are grown in relatively small quantities in Egypt, Sudan, Israel, USA and Peru. The staple length is one of the most decisive characteristics of the cotton fibre because the longer the staple length, the finer the spinnable yarn count. According to the official American standards, the staple lengths are divided into four ranges:

- below 0.99" : short staple

- 0.99" to 1.10": medium staple - 1.11 " to 1.26": long staple

- over 1.26": extra-long staple.

Fibre characteristics

The cotton fibre is characterised by the presence of a cavity in its interior, named ″lumen″. The quality assessment of the cotton fibres is based on following characteristics:

· staple length

· cross-section size, usually called fineness

· linear mass

The spinnability of a fibre, i.e. the finest yarn count attainable in spinning, depends on the length and on the fineness, while the yarn tenacity is related to the strength of the individual fibres as well as to the number of fibres in the yarn cross-section, which has to range between 90 and 120.

The fibre fineness is defined by the American standard ASTM D 123-85 and D 1448-84 as the weighted average linear mass expressed in micrograms per inch, but also in millitex µg/cm. For many years these values were assessed with a gravimetric test method, by weighing measured fibre lengths. For commercial purposes, the linear mass is assessed today more rapidly through special micronaire testing (or similar) instruments.

Besides fineness, a very important fibre property is the maturity degree, which is the ratio between the lumen length and the thickness of the fibre wall.

In fact there is a correlation between fibre maturity, linear mass and micronaire test readings, which is expressed by following values:

- micronaire lower than 3.0 = very fine; maturity degree 0.70-0.80 = immature

- micronaire from 3.0 to 3.9 = fine; maturity degree 0.80-0.85 = maturity below average - micronaire from 4.0 to 4.9 = medium fineness; maturity degree 0.85-0.95 = ripe

- micronaire from 5.0 to 5.9 = coarse fineness; maturity degree 0.95-1.00 = maturity

above average

- micronaire 6.0 and higher = very coarse fineness; maturity degree 1.00 and higher = very ripe

The fibre strength is, like fineness, the property which most affects the yarn characteristics: in fact the two properties are closely connected one another. Owing to the enormous difference in the values of these characteristics among the various fibres, cotton strength is measured with a so-called Pressley tester a flat fibre bundle composed by 500 to 1500 fibres.

For the assessment of fibre quality, also following factors are significant:

- colour: white, slightly spotted, spotted, slightly coloured, yellow stained, slightly grey, grey. The spinner requires anyway colour evenness.

- purity: contents of foreign matters. In fact another requirement of the spinner is the presence of a limited quantity of trash (coarse dusts).

- fibre preparatory process: this corresponds to the ginning process, which is a decisive factor for fibre softness, for uniform and open condition of the tufts and for the persistence of fibre entanglements, called ″neps.

Maturity degree of the cotton fibre— Relationship between lumen width and fibre wall thickness

The typical cotton characteristics all together as colour, foreign matter contents, kind of preparation as well as length and strength contribute to determine the ″grade″ and consequently the commercial value of the fibre, which in the trade is usually referred to as ″good middling″, ″strict middling″, ″middling″, ″low middling″, ″strict good ordinary″ or ″good ordinary″.

Read more...

Cotton | The quality tests

In cotton spinning the cost of the raw material is equal to 50% of the total processing cost.

It is therefore essential that the cotton type selection is based on a wide knowledge of the fibre properties and on the end-item to be produced.

In the last decade the so-called testing lines, which were initially used only by cotton producers and exporters, have been steadily developed and improved, so that they have now been adopted also by the spinning mills; these are driven in this direction by the need to control the quality of the various fibre sources and the reliability of the suppliers, moreover they are attracted by the effective advantages offered by these integrated testing systems, which ensure a closed loop control of fibre characteristics, yarn quality and production process and are focused on the spinning mill's profit. The initials HVI (High Volume Instruments), now well known to all cotton dealers, stand for the kind of instruments which compose the cotton testing lines. These lines offer several advantages:

- measurement of the main characteristics on a cotton fibre bundle: span length as measure of the fibre length, length uniformity, strength, elongation, micronaire as a fineness measure, colour and reflectance, foreign matter (trash) contents. The spinners have asked to add also the SFC (Short Fibre Contents) value which, as already mentioned, has a great impact on the quality of carded yarns. In fact short fibres increase yarn breakages while reducing the yarn tenacity and regularity. The combing process removes the short fibres and originates a quality yarn, but at the expense of a larger quantity of wastes. At least one manufacturer of HVI systems has already the software suited to provide the SFC value from the fibrogram produced by the HVI system. Although the standard error is still about 2%, this procedure allows to identify cotton batches which went through an excessive beating or drying or were too intensively cleaned in the ginning machine.

- possibility of testing up to 180 specimen/h and of checking each single bale. - attainment of reliable test results.

The American cotton growers, under the guidance of USDA (U.S. Department of Agriculture), are making considerable efforts to improve the quality and to reduce the damages caused to the fibre by mechanical picking and ginning. Therefore they were first to equip themselves with these HVI instruments, so that they are in a position to deliver controlled cotton bales with every information which can help the spinner to plan in the best way his production through:

- cotton bale management

- raw material optimisation

- process optimisation with consequent cost reduction.

By bale management we mean the ideal selection of the cotton bales to obtain acceptable technical and economic performance during their processing as well as consistent yarn quality.

By raw material optimisation we mean the result of following operations:

- consistent blending with the support of bales management;

- selection of fibre characteristics according to the requirements of the end-product and based on yarn structure;

- purchase of the most convenient raw material suited to meet the requirements of the end-product.

The process optimisation, on the other hand, depends on following factors:

- selection of the best setting for the drafting rolls;

- optimisation of the processing speeds through comparative trials.

Read more...

What is Cotton stickiness ?

The thorn in the side of the cotton producers and particularly of the spinners, is the notorious honeydew. This term defines the dreadful stickiness of cotton fibres due to the contamination by two terrible insects: the cotton aphid and the white fly, which last is widely spread in case of long dry spells. The researchers have intensified their efforts to control the reproduction of these insects in the last years, during which this infestation increasingly expanded. This spreading of the phenomenon is demonstrated by the result of a survey carried out by ITMF (International Textile Manufacturers' Federation) with 201 spinning mills in 22 countries all over the world about raw cotton contamination: a good 27% of the answers reported as serious the problem of cotton stickiness originated by honeydew, and Sudan was leading the high-risk countries.

Trials are under way to identify the honeydew-affected cotton batches through:

- the analysis of the sugary substances in the honeydew, which cause the cotton stickiness;

- the development of tests on the spot in order to detect the presence of sticky cotton types.

Specific treatments to neutralise cotton stickiness due to honeydew were also studied. Already in 1988 J. Gutnecht explained the results of stickiness tests carried out by ″Minicard″ method to show the influence of the relative humidity in the spinning room on the potential stickiness of a wide range of sticky cotton types and on various blends of sticky and non-sticky materials. At the same time he presented a new thermal method, simpler and less expensive than the Mini-card test, which results correlate pretty well with the Minicard System.

To remove stickiness from cotton fibres, various systems have been used:

- spraying of chemical substances on the fibres, which however causes some problems in subsequent processing

- passage of cotton bales or of a web of opened fibres through high frequency ovens.

In the past years a project was presented by R. Demuth to eliminate the cotton stickiness caused by honeydew. The project consisted in two phases: washing of the fibre with water and detergent with subsequent mild drying followed by thorough drying of cotton in a microwave tunnel, so that the adhesive substances become brittle and are reduced to powder. These systems however are not sufficiently cost-effective, so that there is a trend to dispose of the sticky cotton by mixing it in small percentages with the regular cotton.

Read more...

The cotton stock exchange

The major stock exchanges for cotton trading are situated in New York, Bremen and Tokyo. The cotton price is subject to broad fluctuations, which quite often are due to the seasonal and climatic trend.

Obviously the positive operating results of a spinning mill depend also on a careful and ″lucky″ purchase of the raw material. In this regard we would remind the practice of the purchase option of a ″future″, according to which during the validity of the option the buyer has right, but not the obligation, to turn the option into a ″cotton future″. In practice futures are contracts for the purchase or sale of goods to be delivered at long-term, but at a price established at the time of entering into the contract. There are two possible types of option:

- CALL, : in this case the buyer has the right to convert the option into a long-term

″future″”

- PUT: in this case the buyer has the right to turn the option into a short-term ″future″.

In New York since 1870 the NYCE® (New York Cotton Exchange) take place, which is the world’s leading market for the sale and purchase of cotton futures and options. It is a non-profit-making organisation which assists all segments of the cotton industry by providing the financial means needed for risk management.

Read more...

Polyamide fibres

Polyamide fibres were the first synthetic fibres to appear on the market. They were produced for the first time in USA in 1938, as a result of the research which Wallace H. Carothers had started already a decade before with the objective of preparing through synthesis polymers with a structure similar to that of cellulose and silk. The way followed by Carothers was directed at achieving, as an intermediate material for fibre production, a polymer of hexamethylene diamine adipate (salt N) resulting from the reaction between hexamethylene diamine and adipic acid.

 

 

This end-product was called nylon 6.6, because its two components have 6 carbon atoms each. However, in the same year 1938, Paul Schlack, taking advantage of the error of judgement of Carothers who claimed that caprolactam could not polymerise to form polyamides, succeeded in obtaining all the same a nylon - this time named nylon 6, being made up only of one product with 8 carbon atoms — without infringing the American patents. In the following years, his discovery was extensively exploited in Germany, where the product was called Perlon. Nylon 6.6 and 6 were later produced, under licence or through patent acquisition, also in other European countries, Italy included.

The polyamide fibre was rightly regarded as the "wonder" fibre by virtue of its countless end-uses: stockings and pantyhoses, swimwear, ladies' underwear, corsetry, linings, umbrellas, outerwear, raincoats and floorcoverings. Nylon is also used for several technical applications: tyre cords, conveyor belts, filters, fishing nets, cordage, parachutes, safety belts, inflatable boats and other sport articles.

More recently, this fibre has been further developed to originate continuous filament yarns composed of very fine filaments (abt. 1 dtex) as flat yarns, false-twist textured and air-jet textured yarns, which are used in the production of a new generation of high performance fabrics which meet not only quality and fashion requirements, but also take into account the physiological properties needed by clothing (snowsuits).

This yarn has good dimensional stability to washing, impermeability to water and to air, permeability to steam, good heat transfer, silky and soft handle, good dye yield; all these factors contribute to make this material particularly suited to sport and leisure wear.

The polyamide family includes also other types of nylon: : nylon 4 and 11.

More and more important is becoming the category of polyamide-imides, known also as
aramid fibres. Of relatively recent development, these high-tech fibres, which resist

highest temperatures and even flame and have excellent resistance to chemicals, are suited to technical and industrial uses.

A specialty fibre with optimal comfort properties belongs to the new category of the polyoxamide fibres. This fibre, which is produced in Italy, is particularly suitable for 20- 50% blends with wool, angora, cashmere, alpaca, cotton, viscose staple and synthetics, thus resulting ideal for knitwear.

For dyeing nylon 6.6. usually acid and disperse dyes are preferred, although many other dyestuff classes can be used. Dyestuffs suitable for nylon 6 are disperse and microdisperse, acid, mordant acid, premetallized, synthetic (on the fibre) dyes. The overall world output of polyamide fibres in 1998 was about 4.0 million tons (about 16% of the total production of synthetic fibres altogether).

Read more...

What is Wool ? | Production and consumption

Wool, as all animal hair both coarse and fine, falls under the class of natural fibres and more precisely under the class of animal fibres from hair bulbs. Although the term ″wool″ is commonly associated also with the name of the animals which supply the relevant pile as for instance Angora wool, this term wool stands only for the hair of the domestic sheep (Ovis aies L.) of various breeds.

Archaeologists affirm that sheep existed already when the man appeared on the earth, and it is almost beyond any doubt that wool was one of the first textile fibres available for spinning and weaving. Archaeological finds on the Zagros mountains, at the border between Iran and Iraq, prove that sheep were tamed already 9000 years BC. For a long time, sheep and their products were the main source of wealth and the best medium of exchange. In this connection we remind that the Latin word ″pecunia″ (money) derives from the word″pecus″ (sheep) and that the first coins portrayed this animal.

Wool characteristics depend on following factors:

- method used to obtain the fleece:

virgin wool = wool obtained by shearing the living animal;

plucked wool = wool obtained by chemical treatment of skins of slaughtered sheep - sheep age or sex:

lamb’s wool = first wool sheared from a lamb less than one year old;

ewe’s wool = wool obtained by subsequent shearing;

ram’s wool

- breed:

merino = wool with fineness ≤ 24,5 µ;

cross-bred wool = wool with fineness between 24,5 and 32,5 µ;

coarse wool = wool with fineness > 32,5 µ.

- wool state:

greasy wool, containing the original substances of just shorn wool, i.e. yolk and suint; fleece washed wool, obtained by making the living sheep pass through water; machine scoured wool, in which the grease is to a great extent removed; carbonized wool, that is wool treated with acids and heated to eliminate the contents of vegetable substances; wool tops, that is regular combed silvers composed of parallel long fibres from which all original impurities have been removed, intended for worsted spinning and for high quality products.

Production and consumption

It is estimated that sheep living on earth are today about 1 billion, of which 14% in China, 13% in Australia, 5% in the CIS and 5% in New Zealand. In the last years the production has progressively decreased. For the 1998-99 season a production of 2,4 million tons of raw wool (equal to 1,4 million tons of scoured wool) is expected. According to IWS estimates, the major producing countries of greasy wool in same season 1998-99 are: Australia (681,000 tons), the People’s Republic of China (302,000 t), New Zealand (256,000 tons), CIS (139,000 tons), Uruguay (63,000 t), Argentina (70,000 tons), Turkey (73,000 t), Great Britain (55,000 tons), South Africa (60,000 tons).

Production percentages for the different breeds are: merino 41 %, crossbred 25%, others 34%; 80% of the merino wool is supplied by Australia ad South Africa.

The main producing countries of greasy wool (1997-98)

Read more...

Animal Fibres

The so-called luxury fibres are produced by several different animals: rabbit, mohair goat, cashmere goat, camel, llama (alpaca, vicuna, guanaco) and cattle (yak and musk ox). In recent years a crossbreed, called Cashgora, was obtained by mating the angora he-goat with a wild she-goat. This name was acknowledged by the International Wool Textile organisation (IWTO) only in 1988, but the new wool variety aroused immediately the interest of many Italian spinning mills.

Luxury fibres gad their golden age at the beginning of the 80's; from the middle of the decade, various political and economic factors caused a general recession and a market stagnation. Italian spinners proved however to be real masters in the use of these fibres and especially in constantly creating new blends, making the most of the peculiarities of the woollen preparation and spinning machines "made in Italy".

Hereunder we give some information about the various types of luxury fibres:

- Angora rabbit: the yearly production of about 6,000-7,000 tons takes place mostly in China. The rabbits are clipped up to 4 times a year, thus producing about 250 grams of fibre each. The main market outlets are Japan and Italy. One of the latest developments is a process to produce unfelting angora yarn for handknitting.

- Mohair goat: These animals are bred in South Africa, Texas and Turkey, and it is precisely to the Turkish town of Angora, Ankara today, that they owe their name. The word ″mohair″ which identifies in trade their wool stems from the ancient Arabic word ″Mukhayar″, which means ″glossy goat hair cloth″. In fact the fibre has a rich silken aspect, but has a considerable strength. It is available in relatively large quantities - world production is about 13,000 tons - and is used in both apparel and furnishing. Each goat yields about 4 kg of hair per year. The finest hair coming from goatlings - 24- 25 g - is called kid-mohair. The main consuming countries of this fibre are Japan (25%), Europe and North America. The promotion of this fibre is co-ordinated by the International Mohair Association, which also created a quality trademark.

- Cashmere goat: these animals live in the plains of Central Asia, where climate is ice-cold in winter and hot in summer; just to protect them from cold, their skin gets covered by a thick and soft down (under-fleece down), which is plucked before summer. Each goat yields only 200 g of fibre per year, consequently the total production does not exceed 7,500 tons/year.

- Camel: camel hair is obtained mostly from the camel living in East and central Asia. The main outlet market for this fine, soft and golden fibre is America, where it is used for both woven and knitted fabrics, whereas in Europe it is used mostly for knitwear, especially in men’s garments. Each animal yields about 5 kg of fibre per year. Particularly valuable is the “baby-hair” type. The world production is about 3,000 tons/year.

- Alpaca: these are humpless animals of the camel family living in the Andean regions at heights up to 5,000 m. They are sheared only once every two years and each animal yields from 2 to 4 kg of fleece. This breed produces hair in 14 different natural colours, which is used in knitting and hand knitting yarns in the classic blends alpaca/wool, alpaca/wool/acrylic, alpaca/mohair/wool/acrylic. The alpaca production is about 6,000 tons/year.

- Yak: it is a long-haired ruminant living in Tibet at an altitude of 5,000 m. Its hair is considered as an acceptable alternative to cashmere. It is not produced in commercial quantities and, until 1980, the whole yak hair was exported to Europe and to the United States. At present the Chinese have developed a technology of their own and use directly most of this raw material.

- Musk ox: the underfleece of the musk ox is called “the Arctic’s Golden Fleece” and is probably the rarest and most expensive animal fibre in the world. Declared a protected species in the 30s, the musk ox has been saved from extinction and is today living in herds in North Quebec and in Alaska. Every spring, the animal looses its extremely valuable underfleece, known as ″quiviut″.

Read more...

Silk | History, Production and consumption

Silk is one of the most precious textile fibres of animal origin, obtained from the flossy filament ejected by the silk worm of the butterfly Bombyx mori.

According to tradition, silk was discovered by a young Chinese empress, Hai Ling Shi, in 2640 BC. She noticed in her garden, on the branch of a mulberry tree, a small white cocoon, and brought it into the imperial palace to examine it more closely. Casually she dropped it into hot water and noted that a thin filament began to unwind. The court weaver was asked to do experiments with the new filmy fibre which kept unwinding as the empress pulled it; his trials resulted then in the weaving of the first silk dress.

 

Silk processing aims at obtaining from cocoons a yarn as uniform as possible. It should be pointed out that it is the only continuous filament existing in nature. Raw silk consists by 60-70% of fibroin ( a white coloured protein), by 20-22% of sericin and, for the rest, of gummy substances, minerals and dyestuffs.

Before the pupa changes into a butterfly, cocoons are submitted to a first selection to eliminate the faulty ones and remove their outer layer (floss silk); then they are kept 16- 18 hours in drying ovens to cause the pupa's death and to eliminate moisture which would jeopardize their preservation.

The next operation is the cocoon sieving aimed at removing the residual floss silk, which may however be used together with other types of waste: imperfect cocoons, flock silk, filoselle, broken silk in schappe spinning.

A second sorting is then carried out to divide the cocoons into three size categories, which will be reeled separately because the smaller the filament diameter, the smaller the corresponding cocoon. After softening by immersion in warm water to facilitate the filament extraction, the cocoons are brushed to find the tail end of the filament and to remove from them the top layer of hair (flock silk). Once the tail ends are found, the cocoons are unwound until reeling begins to take place without difficulty. Degumming is followed by filament reeling, which produces a yarn composed of several filaments depending on the required yarn diameter. Once the yarn is twisted, it is wound with helical angle on reels, which are generally contained in special boxes which are closed and heated to enable yarn drying. The dried yarn is packed into skeins and put on the market under the denomination of raw or ecru silk.

Production and consumption

During the past 30 years, the world production of raw silk has steadily grown; this was however associated with a deep change of the production structure in terms of producing countries. In fact in 1970, with a silk world production amounting to abt. 40.000 tons, Japan accounted for the highest share with more than 50% (20,500 tons), followed by China (10,200), Soviet Union (3,000), South Korea (2,850), India (2,250). At that time, Italy still ranked among the producing countries with 310 tons.

On the contrary, today, the estimates of the International Silk Association show a global production of abt. 100,000 tons, where China is the leading producer with 70,000 tons (70%), whereas in Japan the production declined sharply to abt. 4,000 tons (4%). India, with 13,000 t, has therefore overtaken Japan and is now in second position, followed by CIS, Brazil and North Korea.

Among the "other" countries, let us mention Thailand, Turkey, South Korea, Vietnam, Indonesia and Paraguay.

Italy continues to rank among the leading importing countries of raw silk, which is converted, thanks to the skill of its domestic silk industry and to the high-tech Italian machines, into ply and schappe yarns, also blended with other fibres, into silk and bourette fabrics, scarfs, foulards and ties, which have made the Italian design renowned all over the world.

The main silk producing countries (1996)

Read more...